Bayesian, from formula to worldview

Formula

When I was in school, Bayes' formula was one of the few formulas in probability theory that was not covered in high school. I saw it for the first time in undergraduate studies, so I never memorized it. But there is no need to memorize it. According to a common result in conditional probability:

$$\Pr(A|B)\ \Pr(B) = \Pr(B|A)\ \Pr(A)$$

We can get the relationship between $\Pr(A|B)$ and $\Pr(B|A)$

$$\Pr(A|B) = \frac{\Pr(B|A)\ \Pr(A)}{\Pr(B)}$$

This is the Bayesian formula itself.

The denominator is not very interesting, so we usually replace it with the total probability formula, that is, divide the entire probability space $\Omega$ into fully covered but disjoint $\{A_i | \ A_i \cap A_{j \neq i}=\varnothing,\ \bigcup_i A_i=\Omega\}$

$$\Pr(A|B) = \frac{\Pr(B|A)\ \Pr(A)}{\sum_i \Pr(B|A_i) \Pr(A_i)}$$

For any sub-event $A_j$

$$\Pr(A_j|B) = \frac{\Pr(B|A_j)\ \Pr(A_j)}{\sum_i \Pr(B|A_i) \Pr(A_i)}$$

Screening theoretical models based on experimental results

The above is mathematics. In science, let

• A be a set of parameter values of a family of theoretical models, denoted by $Param_k$, and the subscript can be chosen arbitrarily.
• B be experimental observation data, denoted by Ob

$$\Pr(Param_j|Ob) = \frac{\Pr(Ob|Param_j)\ \Pr(Param_j)}{\sum_i \Pr(Ob|Param_i) \Pr(Param_i)}$$

• $\Pr(Param_j)$ represents the prior probability calculated based on the null hypothesis that the jth group of parameters is the correct parameter of the model without experimental verification;**
• $\Pr(Param_j|Ob)$ is called the posterior probability that the jth group of parameters is correct after correction by experimental observations.
• $\Pr(Ob|Param_j)$ has been mentioned in previous articles and is the likelihood of the model parameters under the current measurement data.

And that's what it means: $posterior probability \propto prior probability \cdot likelihood$

For example

The problem of our next-door group can be simplified as follows:

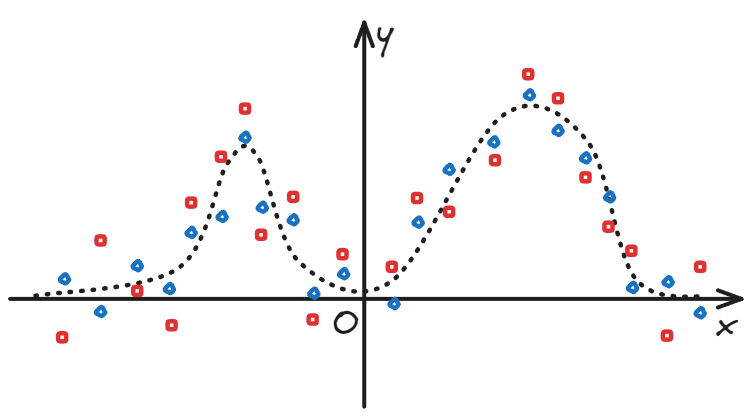
• There are two sets of data (x, y1), (x, y2) that can be fitted by the same family of functions. (Assuming that it is the superposition of two Gaussian functions, $y=f_{A_1,A_2,\mu_1,\mu_2,\sigma_1,\sigma_2}(x) = A_1e^{-\frac{(x-\mu_1)^2}{\sigma_1^2}} + A_2e^{-\frac{(x-\mu_2)^2}{\sigma_2^2}}$
• The errors of the two sets of data are different. (The red data points are obviously farther away from the theoretical value than the blue data points)
• Is there a numerical value that can measure the degree of error of each set of data?

My advice to them is

• Specify the prior probability $\Pr(param_j)=\Pr(A_1,A_2,\mu_1,\mu_2,\sigma_1,\sigma_2)$ based on your professional knowledge. For example, select a range of parameter space, the probability outside the range is zero, and the probability within the range is uniformly distributed.
• $A_1,A_2 \in \left[\min(\{Y_1\}\cup \{Y_2\}),\max(\{Y_1\}\cup \{Y_2\}\right]$
• $\mu_1\in[\min\{X\},\max\{X\}],\ \mu_2\in[\mu_1,\max\{X\}]$
• $\sigma_1,\sigma_2\in[0,\ \Sigma_i\sqrt{|X_i-\bar X|^2/N}]$
• Calculate $\Pr(Ob|Param_j)$ based on some assumptions and statistical laws
• Assume that the error is independent of the x variable and follows a Gaussian distribution with an expectation of 0, $[y_i-f(x_i)]\sim N(0,\sigma^2)$, the standard deviation is estimated based on the residual of each data point minus the model prediction value.
• Assuming that the observations of each data point are independent of each other, $\Pr(Ob)=\Pr(\bigcap_i Ob_i)=\prod_i\Pr(Ob_i)$
• For each set of model parameters, $\Pr(Ob_i|param_j)$ takes the part where the absolute value of the above Gaussian distribution is greater than the absolute value of the residual, which is the area under the line of the tails on both sides of the bell curve.
• After calculating a posterior probability for each set of values in the parameter space, calculate the information entropy of the entire space (see the previous article for the method). For a set of data with a large error, there should be more sets of parameters that can obtain similar fitting results, so that the information entropy is larger.

Worldview

There are three understandings of probability:

• Classical,
• Frequentist,
• Bayesian.

Classical

It is to generalize the classical model and become a general view on possibility - a random event in a random space can be decomposed into several sub-events, and the sub-events can be further divided until the probability of each basic event is equal, which is equal to the reciprocal of the total number of basic events. To calculate a certain event that people are interested in, they only need to count the number of basic events it contains.

It reminds me of the atomic theory of ancient Greece. People at that time believed that the material world was not infinitely divisible. If any material was broken and ground, the process would eventually have an end, and the final product would be the "atoms" of the material. The size of a piece of material is the number of atoms it contains.

Some people criticize this view that it uses possibility to define possibility, which is suspected of circular reasoning. However, looking at the modernized probability theory, probability is defined as a function that satisfies certain conditions. It is axiomatized and the logical chain has a solid starting point, but it is hard to say whether the probability there can still be used as a measure of possibility.

Frequentist

This view can be summed up in one sentence: probability is the limit of frequency when the sample size tends to infinity.

In science (and in everyday life, too, except that people are usually not so precise), measurement errors are inevitable. Even if our measurements are correct, they will be slightly different from each other, not to mention different from the true value to be measured.

The solution is learned in junior high school physics experiments: make multiple measurements, treat the average as (an estimate of) the true value, and calculate the error (confidence interval, p-value, etc.) based on the standard deviation.

Different people (assuming there are M people) can make N measurements on the same observable. For a certain N, no matter what probability distribution the observable itself obeys, the average of these N measurements $\bar X_N$ obeys a normal distribution. This is the central limit theorem (note that it is not the law of large numbers).

When the observable quantity itself also obeys the normal distribution, it will cause the standard deviation (standard deviation) and standard error of the mean (often referred to as standard error) to be easily confused by beginners.

According to this worldview, the true value of a physical quantity is the mean of all possible measurements (all those that have occurred + those that may occur in thought experiments) $\bar X_\infin$.

Because it includes measurements that may have occurred but have not yet occurred, even if the problem we are facing is purely deterministic and there is an objectively definite truth value, no matter how many measurements we have made, we cannot guarantee that we will get the truth value.

Bayes

The aforementioned worldview at least believes that truth exists objectively——

The Bayesian worldview no longer asserts the objective existence of truth values. Every proposition in a scientific theory, whether a priori or a posteriori, is no longer alone, but must be packaged together with all possible alternative theories; it is no longer "correct", but has a degree of credibility measured by probability.

The role of the experiment is no longer to judge right or wrong, but to judge, based on limited prior knowledge (existing scientific theories), to what extent the newly obtained experimental results have updated the credibility weight of each proposition in the old knowledge.

Moreover, each person has different knowledge and different prior probabilities, so when faced with the same experimental data, the updated knowledge system will also be different.

Furthermore, if the prior probability is 0, no matter how significant the experimental data is, the posterior probability must also be 0, so there is nothing you can do about the "unknown unknowns". In practice, no matter how outrageous the prior hypothesis is, as long as you can think of it, you should assign a small initial value that is not 0.