Dynamics[4] | Chaos and its Implication in Truthness and Freedom

Chaos

The definition of chaotic system in our class is:

Aperiodic behavior in deterministic systems that displays sensitive dependence on initial conditions.

I was a lazy student who didn't read much, so I don't know whether this definition was written on the blackboard by our teacher or stolen from the textbook. If it was the latter, our textbook was "Nonlinear Dynamics and Chaos" by Steven H. Strogatz.

Strange attractor

“Non-periodic” means that the dynamic trajectory does not cycle periodically, nor does it converge to a limit cycle or stationary point, so there are other types of attractors, which are called strange attractors.

Saying that a continuous dynamic system is a chaotic system is equivalent to saying that there are strange attractors in the system.

Example: Butterfly Effect

This article is too long, so I will skip the background introduction. In short, it is a dynamic system in the field of meteorology (so in popular science, there is a saying that "a butterfly in the Amazon rainforest occasionally flaps its wings, which can cause a tornado in Texas two weeks later"). After some variable replacement:

$$\begin{cases} \dot x=\mathrm dx/\mathrm dt=\sigma(y-x)\\ \dot y=\mathrm dy/\mathrm dt=rx-y-xz\\ \dot z=\mathrm dz/\mathrm dt=xy-bz \end{cases}$$

The system will change in nature with different values ​​of r.

The Jacobian matrix of the system:

$$\ \mathbb J=\left( \begin{matrix} -\sigma & \sigma & 0 \\ r-z & -1 & -x \\ y & x & -b \end{matrix} \right)$$

• When 0 < r < 1, the stationary point of the system is the origin and is stable;
• When r > 1, the origin becomes an unstable stationary point, and two new stable stationary points appear: $(\sqrt{b(r-1)},\sqrt{b(r-1)},r-1)$ and $(-\sqrt{b(r-1)},-\sqrt{b(r-1)},r-1)$
• When $r>r_H=\frac{\sigma(\sigma+b+3)}{\sigma-b-1}$, chaos begins to appear.
  • The most commonly discussed parameter values ​​are $\sigma=10$, $b=8/3$, at which $r_H$ is about 24.76

两个原本稳定的驻点，此时变成奇异吸引子，在两个维度里构成不稳定极限环，在第三个维度稳定。

对这个系统，像前一篇那样手搓动力学轨迹实在是强人所难了，所以直接把维基百科上的数值模拟结果给偷来：

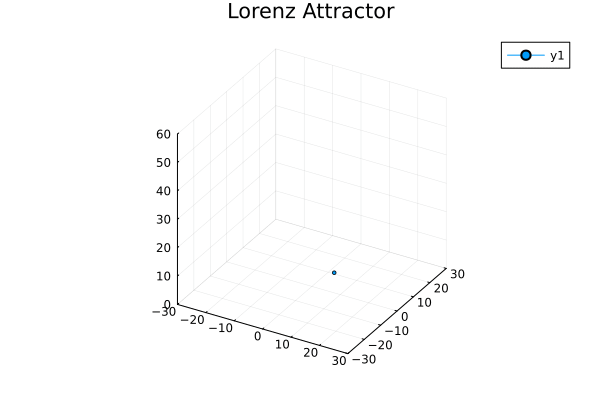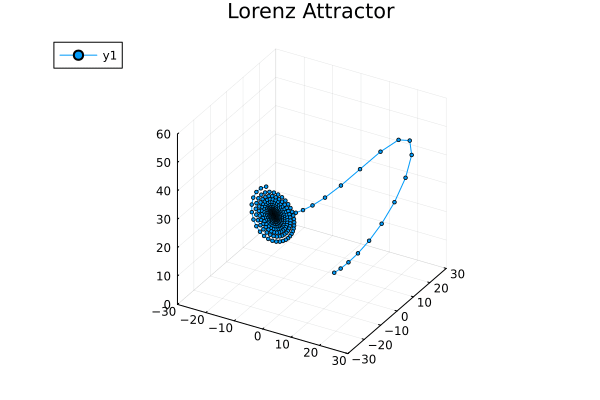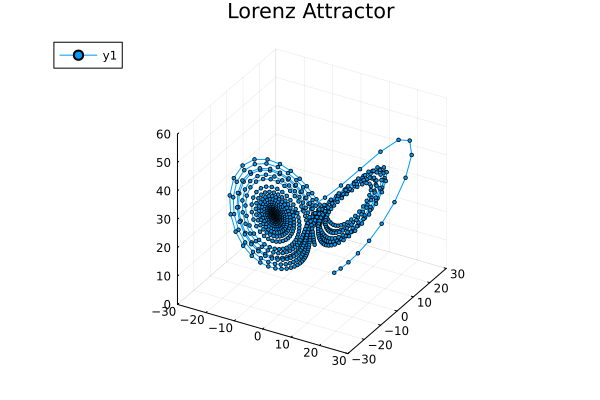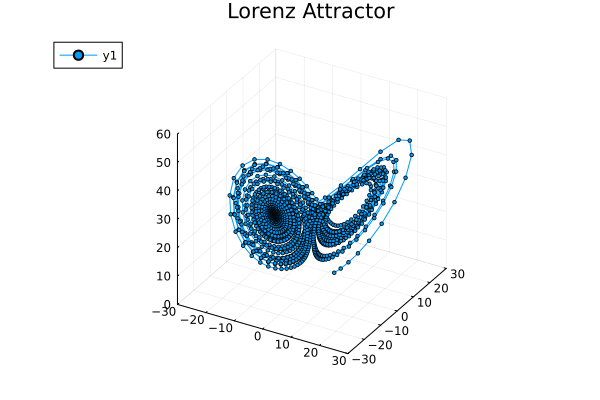
Because any two dynamical trajectories cannot intersect (otherwise the direction of the system at the intersection is unknown at the next moment), it is impossible for the trajectory in a two-dimensional dynamical system to go around a limit cycle for several circles and then suddenly turn around another limit cycle for several circles and then turn back.

The chaos phenomenon of a continuous system** requires at least 3 dynamical dimensions.

Whether the solution is highly sensitive to initial conditions: Lyapunov exponent

The so-called "high sensitivity of the solution to initial conditions" is often measured by the Lyapunov exponent: if two dynamical trajectories are separated by $\delta Z_0$ at the beginning, and $|\delta Z(t)| \approx e^{\lambda t}|\delta Z_0|$ in the subsequent time, $\lambda$ is called the Lyapunov exponent.

Generally speaking, the index is less than 0 in the area dominated by the attractor, and greater than 0 in the area dominated by the repeller.

The "strangeness" of the strange attractor is that although it is an attractor, the Lyapunov exponent is greater than 0.

In this way, two initial conditions of the same system that are "slightly different" will be "far apart" after a period of time, so "the solution is highly sensitive to initial conditions".

import numpy as np
import matplotlib.pyplot as plt

dt    = 1E-4
N     = int(2.5E5)
delta = 1E-2

sigma = 10
b     = 8/3
r     = 26

f = lambda x,y,z: np.array([
                        sigma * (y - x),
                        r*x - y - x*z,
                        x*y - b*z
                  ])

XYZ0 = np.empty((3,N+1))
XYZ1 = np.empty((3,N+1))
XYZ0[:,0] = np.array([-10.0     ,-10.,20.])
XYZ1[:,0] = np.array([-10.+delta,-10.,20.])
for t in range(N):
    XYZ0[:,t+1] = XYZ0[:,t] + f(*XYZ0[:,t])*dt
    XYZ1[:,t+1] = XYZ1[:,t] + f(*XYZ1[:,t])*dt

plt.figure()
plt.xlabel(   "$t$",fontsize=16)
plt.ylabel("$x(t)$",fontsize=16)
plt.plot(np.arange(N+1)*dt, XYZ0[0], label="$x_0=10.0$")
plt.plot(np.arange(N+1)*dt, XYZ1[0], label="$x_0=9.99$")
plt.legend()
plt.show()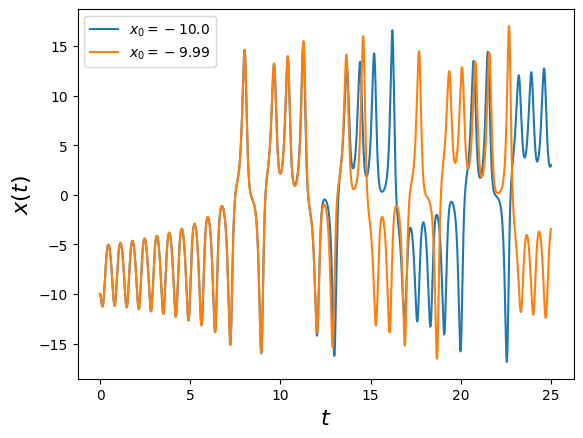

Why "the solution is highly sensitive to the initial conditions": the dimension of the attractor

But on the other hand, the attractor attracts the dynamic trajectory to a subset of the phase space, so the distance between adjacent trajectories should be shrinking over time. In a dynamic system $\dot{\vec z}=\vec f(\vec z)$, let the "volume" occupied by a bunch of initial conditions in the phase space be $V_0$, and the rate of change of this volume over time is calculated as follows:

$$\frac{1}{V}\frac{\mathrm dV}{\mathrm dt}=\vec\nabla\cdot\vec f$$

Substituting the Lorentz system into the above formula, $V(t)=V_0e^{-(\sigma+1+b)t}$ does decrease over time, and can even be as small as 0.

In ordinary attractors, stable stationary points have 0 dimensions and stable limit cycles have 1 dimension, which are at least one whole dimension lower than the dynamic system in which they are located.

With numerical simulation, people figured out that the dimension of the Lorenz attractor is about 2.05, which is not an integer.

Fractional dimensions are often related to fractal structures. The Lorenz attractor still occupies a certain space when its volume is 0 (this is more obvious in discrete dynamic systems), and the adjacent trajectories near the attractor may evolve into different branches of the fractal, giving the Lyapunov index a chance to be greater than 0.

Truthness

“The solution is highly sensitive to the initial conditions”, so what?

In most popular science articles, the description of chaotic systems stops at repeating “the solution is highly sensitive to the initial conditions”, and there is nothing more to it. Just like a poor student writing a literature review, he dare not understand it on his own, for fear of being accused of a straw man fallacy.

The meaning of chaos needs to be understood in conjunction with the “falsifiability” demarcation standard mentioned in :

Since the $\delta Z_0$ between two initial conditions can be arbitrarily small, we can always find two trajectories whose initial values ​​differ by less than the error of the measuring instrument. At this point, the assertion that “their initial values ​​are different” cannot be falsified, and we can only assume that they are equal.

However, over time, the difference in their dynamical trajectories will increase to a level significantly greater than the measurement error.

At this point, it becomes "for one experimental input, the theory will give multiple completely different assertions of long-term behavior, and it is impossible to determine which one is correct." Only by considering experimental errors can we get the "unpredictability" in the definition of chaos.

This unpredictability is not due to the failure of the theory. If the theory cannot be used to describe the current system, you cannot assert that there are strange attractors here, and you cannot assert that there are chaotic phenomena.

This unpredictability is not due to the floating point error of the numerical simulation. If the floating point error causes the numerical solution to be unable to be approximately equal to the true solution, then this numerical simulation should not be used. If a scientific outreach work about chaos falls into the rabbit hole of computer floating point numbers and "pseudo-random numbers/true random numbers", then this outreach is likely to fail.

Newtonian Mechanics ≠ Fatalism

Chaotic phenomena arise from complex systems, but this "complexity" does not need to be particularly complex. The simple pendulum composed of a hard stick ball in the hand-rubbing phase diagram in the previous article can become a chaotic system as long as a free-swinging hard stick ball is hung under the hard stick ball, and this is just a system completely dominated by Newtonian mechanics.

After the establishment of the Newtonian mechanics system, Laplace imagined a fairy (Démon de Laplace) that knows the exact position and momentum of every atom in the universe at the current moment. Laplace believes that the fairy can know the world at any time from the past to the future. The supernatural phenomenon encountered by Futaba Rio in "Rascal Does Not Dream of the Witch of Reason" is a kind of use of Laplace's demon by the light novel author.

Now we can refute that the information about the position and speed of all matter in the universe obtained by Laplace's fairy cannot have infinite precision (after all, infinity is not a number), so chaos will still make the long-term future of the universe unpredictable.

This is "epistemology does not imply fatalism".

Appeal to quantum mechanics?

When trying to save Laplace's demon, the usual idea is that Newtonian mechanics is not applicable to microscopic systems. To describe motion at the atomic scale, quantum mechanics is needed, and quantum mechanics is fundamentally probabilistic, not deterministic.

However, the Copenhagen interpretation of quantum mechanics includes the "correspondence principle": the quantum physical behavior of large-scale macroscopic systems should be similar to classical behavior.

When the number of microscopic particles reaches the order of magnitude of Avogadro's constant, the order of magnitude of the physical processes between particles will only be higher. These processes constitute "observations" of neighboring systems and cause each other to decoherence. The difference between the predictions of quantum mechanics and classical mechanics will eventually converge to the error range of macroscopic measuring instruments.

Classical mechanics often does not assert those novel physical phenomena that can only be explained by quantum mechanics, so quantum mechanics is a supplement and paradigm update to classical mechanics, not a falsification.

After all, classical mechanics is a science, not pure mathematics, and its correctness is guaranteed by experiments. Since experiments verify and do not falsify, the explanation that is deterministic and unpredictable still needs to be given within classical mechanics.

Gödel's Incompleteness Theorem

Gödel's incompleteness theorem states that a logical system that includes Peano's axioms (the mathematical basis of natural numbers) cannot be both self-consistent and complete. That is to say, almost all quantitative theories either have internal contradictions (a proposition and its negation are both judged to be correct by the theory), or there are correct propositions that are not included in the theory.

Mathematics and natural sciences have chosen to resolutely eliminate internal contradictions, so they inevitably have to admit their own limitations. Knowing that "their knowledge is boundless" and that they can never exhaust all true propositions, they still devote their limited lives to it, "even throwing a grain of sand into the treasure house of human knowledge is great" (Marie Curie).

But on the other hand, the propositions of natural science need to be universal. Scientific propositions should be universal propositions, and any concessionary ad hoc amendments need to increase the falsifiability of the proposition, otherwise it is pseudoscience.

Chaotic systems have become a way to reconcile the two. A physical law is equivalent to the set of all solutions that satisfy this law, and a specific physical process is just an element in the set. The correctness and knowledge of the former does not necessarily enable people to choose any of the latter.

Similar results can also be found in Prof. Kaihua Zhao's discussion of "the symmetry principle when the cause cannot uniquely determine the result" in "Qualitative and Semi-Quantitative Physics".

Freedom

We often see expressions like "knowledge is freedom" and "knowledge makes people free", but if you think about it carefully, these propositions use similar words, but the meanings they express are very different.

Knowledge itself is not freedom.

On the contrary, knowledge will eliminate freedom. An originally free choice, now knowledge tells you that some of its options are right and others wrong, and there are advantages and disadvantages after you choose. As long as the knowledge is correct and has not been falsified, not choosing the optimal solution given by knowledge will result in loss/less profit, which is what economics calls opportunity cost.

Knowing that you will suffer a loss in advance but still doing it, and accepting the consequences calmly after doing it, this is the category of civil disobedience, which is the freedom given to you by values ​​beyond knowledge. Of course, it can also be said that values/virtues are a kind of knowledge (Socrates), but this kind of moral knowledge is different from objective science after all.

On the other hand, knowledge does make people free.

The understanding of knowledge includes the understanding of its applicable boundaries. Outside the boundaries, the right and wrong, advantages and disadvantages of each option cannot be determined by knowledge, and the choice there is still free in the scientific sense.

More knowledge will reveal more "known unknowns" like chaotic systems, expanding the scope of freedom. Where exactly is freedom and what we don't know, it also requires the person who claims to provide evidence.

The counter-selection method of "we know nothing except what we know" has very little amount of information even if it is correct. Zhuangzi and Huizi might have been smart in one moment and one matter when they argued philosophically on that river, but over thousands of years, it is the people who performed down-to-earth studies that accumulate small steps to reach a thousand miles.

What's next

Besides phase portrait and dynamical trajectories, there is at least another half of qualitative and semi-quantitative analysis of dynamics, which is phase diagram and bifurcation of dynamical systems.

Besides continuous systems, there is at least another half of dynamical systems, which is discrete systems represented by recursive mappings, where chaos may occur in one dimension.