.m | Bayesian 贝叶斯，从公式到世界观

公式

我上学的时候，贝叶斯公式是概率论里面，少数高中完全不涉及，到了本科才第一次见的公式，所以我从来没背下来过。不过也用不着背，根据条件概率里面的一个平凡结果：

$$\Pr(A|B)\ \Pr(B) = \Pr(B|A)\ \Pr(A)$$

可以得到 $\Pr(A|B)$ 和 $\Pr(B|A)$ 之间的关系

$$\Pr(A|B) = \frac{\Pr(B|A)\ \Pr(A)}{\Pr(B)}$$

这就是贝叶斯公式本体。

分母没什么意思，所以一般我们要用全概率公式替换，也就是把整个概率空间 $\Omega$ 划分为全覆盖但是不相交的 $\{A_i | \ A_i \cap A_{j \neq i}=\varnothing,\ \bigcup_i A_i=\Omega\}$ （之前写错了，这里的 $A_i$ 和上文的 A 没有关系）

$$\Pr(A|B) = \frac{\Pr(B|A)\ \Pr(A)}{\sum_i \Pr(B|A_i) \Pr(A_i)}$$

其中任意一个子事件 $A_j$

$$\Pr(A_j|B) = \frac{\Pr(B|A_j)\ \Pr(A_j)}{\sum_i \Pr(B|A_i) \Pr(A_i)}$$

根据实验结果筛选理论模型

以上是数学。在科学中，令

• A 为一族理论模型的一组参数取值，记为 $Param_k$，下标可任意选取。
• B 为实验观测数据，记为 Ob

$$\Pr(Param_j|Ob) = \frac{\Pr(Ob|Param_j)\ \Pr(Param_j)}{\sum_i \Pr(Ob|Param_i) \Pr(Param_i)}$$

其中

• $\Pr(Param_j)$ 表示第 j 组参数是模型的正确参数的，未经实验验证，根据零假设计算的 先验 (prior) 概率；
• $\Pr(Param_j|Ob)$ 叫做经过实验观测修正之后的，第 j 组参数正确的 后验 (posterior) 概率。
• $\Pr(Ob|Param_j)$ 在之前的文章中讲过，是当前测量数据下，模型参数的 似然性 (likelihood)。

$$posterior \propto likelihood \cdot prior$$

举个例子

隔壁组的问题可以简化为下图：

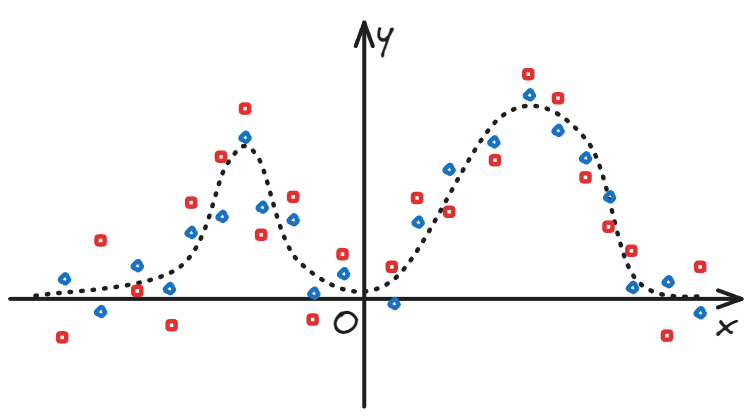
• 有两组数据 (x, y1), (x, y2) 可以用同一族函数来拟合。（假设为两个高斯函数的叠加，$y=f_{A_1,A_2,\mu_1,\mu_2,\sigma_1,\sigma_2}(x) = A_1e^{-\frac{(x-\mu_1)^2}{\sigma_1^2}} + A_2e^{-\frac{(x-\mu_2)^2}{\sigma_2^2}}$
• 两组数据的误差不同。（红色数据点显然比蓝色数据点，相对于理论值偏离得更远一些）
• 问有没有一个数值，可以衡量每组数据的误差程度。

我给他们的建议是

• 根据自己的专业知识指定先验概率 $\Pr(param_j)=\Pr(A_1,A_2,\mu_1,\mu_2,\sigma_1,\sigma_2)$。比如选定一个参数空间的范围，范围之外概率为零，范围之内均匀分布。
  • $A_1,A_2 \in \left[\min(\{Y_1\}\cup \{Y_2\}),\max(\{Y_1\}\cup \{Y_2\}\right]$
  • $\mu_1\in[\min\{X\},\max\{X\}],\ \mu_2\in[\mu_1,\max\{X\}]$
  • $\sigma_1,\sigma_2\in[0,\ \Sigma_i\sqrt{|X_i-\bar X|^2/N}]$
• 根据一些假设和统计规律计算 $\Pr(Ob|Param_j)$
  • 假设误差与 x 变量无关，服从期望为 0 的高斯分布，$[y_i-f(x_i)]\sim N(0,\sigma^2)$，标准差根据各数据点减去模型预测值的残差估计。
  • 假设每个数据点的观测相互独立，$\Pr(Ob)=\Pr(\bigcap_i Ob_i)=\prod_i\Pr(Ob_i)$
  • 对于模型的每一组参数 ，$\Pr(Ob_i|param_j)$ 取上述高斯分布的绝对值大于残差绝对值的部分，就是钟形曲线两侧尾巴的线下面积。
• 对参数空间中的每一组值都算出一个后验概率之后，计算整个空间的信息熵（方法见之前的文章）。误差较大的一组数据，应当有更多组参数可以获得类似的拟合结果，从而信息熵更大。

世界观

对于概率，有三种理解：

• 古典的 (classical)、
• 频率学派的 (Frequentist)、
• 贝叶斯的 (Bayesian).

古典

就是将古典概型推广，成为一种关于可能性的普遍观点——一个随机空间里的随机事件可以分解成若干子事件，子事件还可以再分，直到每个基本事件的概率相等，都等于基本事件总数的倒数，而要计算人们感兴趣的某一事件，只需要数出其包含的基本事件的数量就行了。

让人联想到古希腊古典时代的原子论。时人认为物质世界也不是无限可分的，将任意一种材料打碎研磨，这一过程最终会有一个终点，最终的产物就是这种物质的“原子”。一块材料的大小，就是其所含原子数量的多少。

有人批评这种观点用可能性去定义可能性，有循环论证谬误之嫌。但是看现代化了的概率论，概率被定义成了满足某些条件的函数，公理化是公理化了，逻辑链条是有了坚实的起点，但是那里的概率还能不能被当作可能性的度量，实在是不好说。

有人批评这是机械唯物主义，这种人批判的武器一般是武器的批判，别争辩，先活下来再说。

频率学派

这种观点一言以蔽之：概率是频率在样本量趋于无穷时的极限。

科学中（日常生活中也一样，只是人们通常没这么精确），测量误差不可避免，我们每一次的测量哪怕正确，互相之间也会有细微的差别，更不用说和待测的真实值不同了。

解决方法在初中物理实验里学过：多次测量，把平均值当作真值（的估计量），根据标准差计算误差（置信区间、p 值等等……）。

不同的人（假设有 M 个）可以对同一个可观测量进行 N 次测量，对于一个确定的 N，不论这个可观测量本身服从何种概率分布，这 N 个测量值的平均数 $\bar X_N$ 都服从正态分布，这就是中心极限定理（注意不是大数定律）。

当可观测量本身也服从正态分布的时候，就会导致标准差 (standard deviation) 和标准偏误 (standard error of the mean, 常简称为 standard error) 容易让初学者混淆。

而按照这种世界观，所谓一个物理量的真值，就是所有可能的（所有已经发生过的+思想实验中可能发生的）测量的均值 $\bar X_\infin$。

因为包括可能发生还未发生的测量，所以哪怕我们面对的问题是纯决定论的，客观存在一个确定的真值，无论我们已经进行过多少次测量，都无法保证得到真值。

有人批评这是客观唯心主义，这种人批判的武器一般是武器的批判，别争辩，先活下来再说。

贝叶斯

前述世界观好歹还认为真值客观存在——

贝叶斯世界观则直接不再对真值的客观存在下断言，不论先验还是后验，科学理论里的每一条命题，都不再孤单，而是要和所有可能的替代理论打包在一起；也不再“正确”，而是具有一个以概率衡量的可信程度。

实验的作用不再是判断对错，而是在有限的先验知识（现存的科学理论）下，判断新取得的实验结果在多大程度上，更新了旧知识里每条命题的可信权重。

而且每个人掌握的知识不同，先验概率不同，在同样的实验数据面前，所更新出来的知识体系也会不同。

再者，如果先验概率为 0，任你实验数据如何显著，后验概率也一定为 0，所以对“未知的未知”无能为力。实践中，再离谱的先验假设，只要能想到，也要赋一个小而不为 0 的初值。

有人批评这是主观唯心主义，这种人批判的武器一般是武器的批判，别争辩，先活下来再说。

送分题

已知本省不超过二十个地级行政单位。一中是本市最好的高中，本科过线人数年年创新高。

已知本市报纸会公布喜报，上有全市前若干名学生的姓名、分数、录取学校等信息。省招办有根据成绩取得全省排名的服务。比如某年本市第十名，全省排名两千名开外。

你能否据此评价母校和家乡的教学质量，以及本省各地区之间教育水平的平均程度？

你该如何评价，从定义原假设和备择假设，到用何种概率分布对先验概率建模？

你有资格评价吗？