动力学的终极目标，就是给出感兴趣的物理量随时间变化的函数，时间至少是这个函数的自变量之一。

    公元 1644 年，清政府钦天监的官员和西来的传教士打赌，看谁能更准确地预测即将到来的日食，当然要提前给出答案，日食发生时验证。

    这并不代表当时的传教士和钦天监官员们都精通科学哲学里的可证伪性，但足以说明时间的公信力，对于那些科学一说结论就马上“啊对对对我本来就这么想的”的南郭先生的筛选力——

    动力学方程的标准形式

    动力学的终极目标，就是给出感兴趣的物理量随时间变化的函数 z=z(t,… )z=z(t,\dots)，时间至少是这个函数的自变量之一。

    对付上述的时变函数，需要根据实验现象写出上述函数应该满足的数量关系，连续函数一般包含对时间的导数，离散数列一般包含递推关系（比如马尔科夫链）。写成的等式，就是动力学方程。

    动力学方程的标准形式，是若干微分方程的联立，而且都是对时间的一阶导数，而且都只出现在等号的同一边：

    {z˙1=dz1/dt=f1(z1,z2,…zn)z˙2=dz2/dt=f2(z1,z2,…zn)…z˙n=dzn/dt=fn(z1,z2,…zn)\begin{cases} \dot z_1=\mathrm dz_1/\mathrm dt = f_1(z_1,z_2,\dots z_n) \\ \dot z_2=\mathrm dz_2/\mathrm dt = f_2(z_1,z_2,\dots z_n) \\ \dots \\ \dot z_n=\mathrm dz_n/\mathrm dt = f_n(z_1,z_2,\dots z_n) \\ \end{cases}

    如果等号右边的所有 f 都是各物理量的线性组合，这样的动力学系统叫做线性系统，整个方程组可以写成矩阵乘法 z⃗˙=ddtz⃗=J z⃗\dot{\vec z} = \frac{\mathrm d}{\mathrm dt} \vec z = \mathbb J\ \vec z；不然则称为非线性系统。

    描述一个动力学系统所需要的标准形式方程的最低数量，叫做这个系统的自由度，n 个自由度的系统叫做 n 维动力学系统。一维动力学系统就是单个标量方程 z˙=dz/dt=f(z)\dot z = \mathrm dz/\mathrm dt = f(z)

    写上面这句话的时候感觉有点不对，因为一般物理学系统的自由度是变量的数量减去方程的数量。后来想到一个解释：z˙n\dot z_n 们也是变量（广义动量），所以 n 个方程有 2n 个变量，自由度 2n － n = n

    另外要注意的一点是，此处讨论的空间是相空间 (phase space)，也就是动力学系统的广义坐标张成的数学上的空间，而不再是普通人日常所说的那个现实物质所存在的空间。

    这个区别，是绝大多数的物理科普作品没能向大众传递正确信息的原因。其中还有故意误导者，对付这种人，听见它们扯“空间”、“维度”的时候就赶紧捂好钱包吧……

    形式不标准怎么办

    当然，并非所有的动力学系统都能写成这么标准的形式——

    如果动力学函数 f 本身包含时间作为变量，那就在上述方程后面追加一个维度 t˙=dt/dt=1\dot t=\mathrm dt/\mathrm dt=1

    如果动力学方程中存在某个量对时间的高阶导数，可以引入 n－1 个中间变量，把一个 n 阶微分方程变成 n 个一阶微分方程——

    比如牛顿第二定律，F = ma，加速度是位置对时间的二阶导数，所以为了塞进我们这套话语体系，需要额外定义位置对时间的一阶导数作为中间变量，也就是速度 v.

    {v˙=dv/dt=F/mx˙=dx/dt=v\begin{cases} \dot v=\mathrm d v/\mathrm d t = F/m \\ \dot x = \mathrm d x/\mathrm d t = v \end{cases}

    如果以上化简都不管用，对时间的高阶导数还是和 f 绞在一起，此时 z 满足的函数叫做 隐函数，对于数学家来说也许不雅观，不过对于搞物理的，反正都要上数值模拟了还穷讲究什么……

    为什么力学到加速度为止

    因为牛顿第二定律是一个二阶微分方程，而我们一般只讨论保守力场。

    这两者一起导致了其标准形式只包含两个一阶时间微分方程，每个现实空间维度只需要两个广义坐标（位置 xx、速度 vv），两个广义速度（速度 x˙\dot x、加速度 v˙\dot v），更高阶的导数不出现。

    反过来说，如果力场不保守，势能场本身包含了位置对时间的高阶导数，那么这个动力学系统就确实需要比加速度更高阶的导数。这样的系统不满足能量守恒（有外来能量输入或对外做功），但不是不能存在。

    之前看中科院物理所的公众号转发了一篇知乎文章《牛顿第二定律：真的塞不下了》，原文在哈密顿力学里搞了半天，整了个“能量没有下界”的反证法。

    这种证明牛顿第二定律的理论游戏，给人一种搞理论搞魔怔了的感觉……

    牛顿第二定律是经典力学的公理，公理就是不证自明的（原文的靶子“但当我们向我们的力学老师提出疑问时，得到的答案往往是‘这是实验总结出的规律’”反而是最正确的解释～）

    作为其他定理的证明起点，反过来说是没办法在逻辑体系内部证明的，证明必有循环推理谬误。（好像还有很多人以为逻辑闭环很牛逼是吧～）

    原文究竟是在哪一步完成这种偷渡的，恕我水平有限，没看出来。（初步怀疑是对高阶系统直接用欧拉-拉格朗日方程犯了类比谬误。）

    这篇知乎文章是一个三部曲的最后一篇，反而是物理所没转发的前两篇教育意义更大一些……

    “四大力学”

    《理论力学》《量子力学》《电动力学》《热力学和统计物理》四门课，因为课名里都有“力”“学”两个汉字，被不少人合称为“四大力学”。

    之前曹则贤老师写了一篇文章《“四大力学”的错误说法可以休矣》试图正本清源。

    这四门课当然不是“力的学问”，但是这四门课也并非没有共性，他们都是本文所讲的动力学系统。

    • 理论力学研究的是位置和速度（说动量是为了更顺滑地和量子力学及相对论衔接）的动力学，
    • 量子力学研究的是位置和速度的概率振幅的动力学，
    • 电动力学研究的是电场和磁场的动力学，
    • 热力学和统计物理研究的本应是热运动的动力学，但由于统计工具有限，物理专业信息论教的也少，能写进课本的基本都在动力学系统的驻点上做文章，显得不太“动力学”

    至于说可以休矣，我觉得恰恰相反，越是这种不完全正确的说法，越可以在修正之后多说——

    毕竟完全正确的事情，谁说都是正确的，那我说出来又能显出什么本事呢？

    而不完全正确，想讨论又绕不开的说法，才是文明话语权的体现。为什么叫四大力学？因为在汉语里它们的词根是相同的。这话一说出来，多么威风！

    当然你要知道这里的“力学”是 dynamics，不是 study of forces，所以坚持是对的，纠正也是对的，纠正是为了更好地坚持～

    两次世界大战欧洲自相残杀，将文明领袖的位置拱手让人，于是美苏沐猴而冠，却之不恭。但其德不配位，遂有“世界上最好的高中水平科学教育在美国，但是在美国大学”的段子。这样的话语权输出机会，以后还有很多。

    要是这篇文章早两天写完就好了，现在伟大的特朗普总统已经把文明世界灯塔的谜底揭开，哦，我的好伙计们，显得我有点事后诸葛亮……

    下集预告

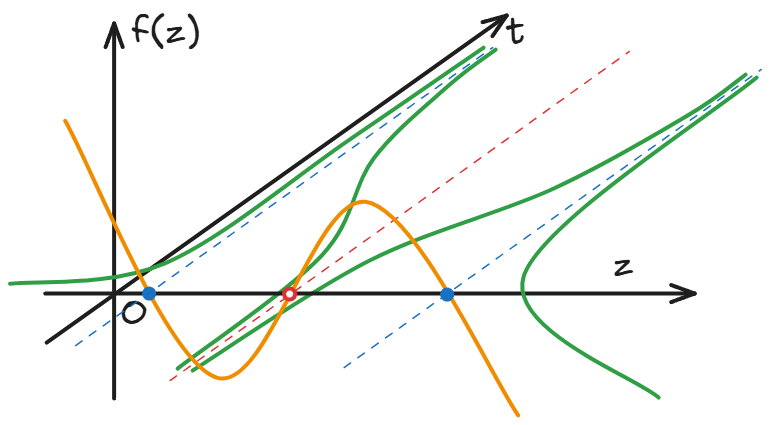
    以一维非线性动力学系统为例，介绍一下动力学系统的若干概念，以及定性和半定量分析框架。

    本文收录于以下合集：