动力学[5] | 离散系统的动力学

本系列的 [1] 到 [4]，以单篇尽量不超过微信公众号读者脑容量期望值的篇幅，构建了从动力学入门到混沌现象的最小逻辑链条，尽力避免了横生枝节。

之前方向过于明确，思路过于流畅，这就导致之后再写什么成了问题。两个方向：

1. 递推映射表示的离散系统。此方向的远期目标，是了解华人数学家李天岩提出的“周期 3 意味着混沌”的上下文。
2. 动力学定性和半定量分析的剩余部分，包括相图 (phase diagram)、动力学系统的分岔 (bifurcation)、临界现象 (criticality)。此方向的远期目标，是能欣赏 Thierry Mora 和 William Bialek 合著的论文《Are Biological Systems Poised at Criticality?》

先写前者，会导致很多概念无法讨论，浮于表面；

先写后者，会缺少一半的例证，毕竟连续系统和离散系统的性质有所不同，前者里的有些结论并不能平移到后者。

Whatsoever——

递推映射 (iteration map)

离散系统讨论的变量 x 不再是实数时间 $t\in \mathbb R$ 的连续函数 x(t)，而是以自然数 $i\in \mathbb N$ 为变量的函数，更常见的表示法是数列 $[x_i]$

描述数列常用的方式是通项公式，这也是离散系统追求的目标。

但是在物理问题中，更容易得知的是相邻若干项之间的关系，即递推公式

$$x_{n+1} = g(x_n)$$

举个例子：方程的数值解

上面公式里的函数 g 不同于连续系统中的 f。

首先是两者的量纲不同：g 的量纲是 [x]，f 的量纲是 [x]/[t]。

另外数量级也不同：$f(x)\sim O(x_{n+1}-x_n)$，$g(x_n)\sim O(x_{n+1})$

熟悉数值分析的朋友应该能联想到解数值方程 f(x)=0 的驻点迭代法 (Fixed Point Iteration)：

1. 将 $f(x)=0$ 改写为 $x = g(x),\ g(x)=x-f(x)$
2. 选取一个猜测起点 $x_0$
3. 重复计算 $x_{n+1}=g(x_n)=x_n-f(x_n)$
4. 直到 $|x_{n+1}-x_n|<\epsilon$

以上方法要求 x 是 g 的一个稳定驻点，若是不稳定的话，需要迭代 g 的反函数 $g^{-1}$。稳定的含义见后面的小节。

要是你们的计算物理老师沉迷于翻转课堂的话，以上内容联想不到也没关系～

图上作业

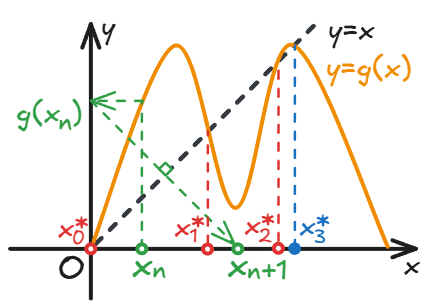
不失普遍性，我们以金拱门形状的递推函数为例。

先在 x-y 坐标系下画出 y = x 和 y = g(x) 的图像，即图中黑色虚线和黄色实线。

动力学轨迹

即图中按先后顺序排列的的绿色圆点。

绿色虚线给出了在图上随时间演化的作图法：

1. 把 $x_n$ 标在 x 轴上
2. 过 $(x_n,0)$ 作一条竖直线，与递推函数交于 $(x_n,g(x_n))$
3. 过 $(x_n,g(x_n))$ 作一条水平直线，与 y 轴交于 $(0,g(x_n))$
4. 过 $(0,g(x_n))$ 作一条与 y = x 垂直的直线，与 x 轴交点的横坐标即为 $x_{n+1}$
5. 把 $x_{n+1}$ 代入步骤 1……

因为没有了连续性的束缚，两个不同的动力学轨迹之间可以交叉——甚至“交叉”这个概念就是不存在的，离散动力学变量随时间的变化应该用散点图表示，在数据点之间连线是没有意义的。

驻点

即 x 轴上并非绿色的各个圆点。

含义和连续系统一样，是动力学变量一旦到达就不会再变化的值。

计算方法是解方程

$$x = g(x)$$

图上就是递推函数图像和直线 y = x 交点的横坐标。

图中的例子可以看出，动力学轨迹可以跨越驻点。这也是没有连续性的束缚导致的。

稳定性

图中蓝色实心圆点表示稳定驻点，红色空心圆点表示不稳定驻点。

稳定的计算方法是在驻点处解不等式

$$|g'(x^*)| < 1$$

这个标准在图上需要比连续系统多费一番思考才能得到直观的理解。

例子

逻辑斯蒂映射 (logistic map)

$$x_{n+1} = g(x_n) = r x_n (1-x_n)$$

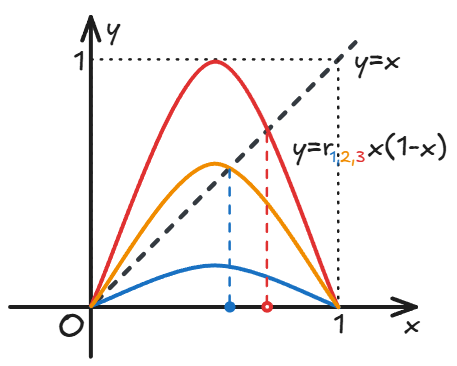
这个模型受生物种群数量随代际变化的启发。种群数量越多，繁殖基数越大；种群数量越少，生存空间越多。模型的表现受到参数 r 的调控：

• r ≤ 1: 一个驻点 x* = 0，稳定
• r > 1: 两个驻点 x* = 0 和 1 - 1/r，其中 x = 0 总是不稳定，而 x = 1 - 1/r
  • 1 < r < 3: 稳定
  • r > 3: 不稳定，某些取值会出现混沌现象

洛伦兹映射 (Lorenz map)

$$\begin{array}{rl} g(x)= & \bigg\{\begin{array}{ll} 2x, & x\le 1/2 \\ 2-2x, & x\gt 1/2 \end{array} \\ g^2(x)= & g\left(g(x)\right) \end{array}$$

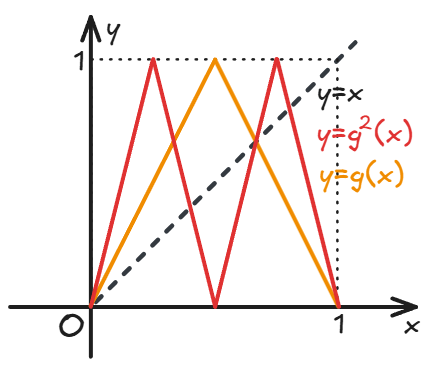
这个例子的重点在于 $g^n(x)$ 的操作在以后的讨论中还会用到。计算高阶驻点的稳定性的时候要用到链式法则

$$\left|\frac{\mathrm d^3g(x)}{\mathrm dx}\right|=\left|\frac{\mathrm dg}{\mathrm dx}\right|_{g^2(x)}\left|\frac{\mathrm dg}{\mathrm dx}\right|_{g(x)}\left|\frac{\mathrm dg}{\mathrm dx}\right|_{x} = 2^3$$

Lorenz 证明，如果初值条件 $x_0$——

• 是一个有理数，则序列存在周期；
• 是一个无理数，则序列呈现混沌现象。