相图 (phase portrait) 常用来描述动力学系统的定性和半定量行为,比如驻点及其稳定性
动力学方程
上回书说到——
动力学方程的标准形式,是若干微分方程的联立,而且都是对时间的一阶导数,而且都只出现在等号的同一边:
举个例子,现在来考虑一个一维动力学系统
相图 (phase portrait)
除了语言和公式,相图 (phase portrait) 也常用来描述动力学系统的定性和半定量行为,就像下图这样:

对于二维动力学系统, 往往用箭头向量场标注(比如用 matplotlib 中的 streamplot);
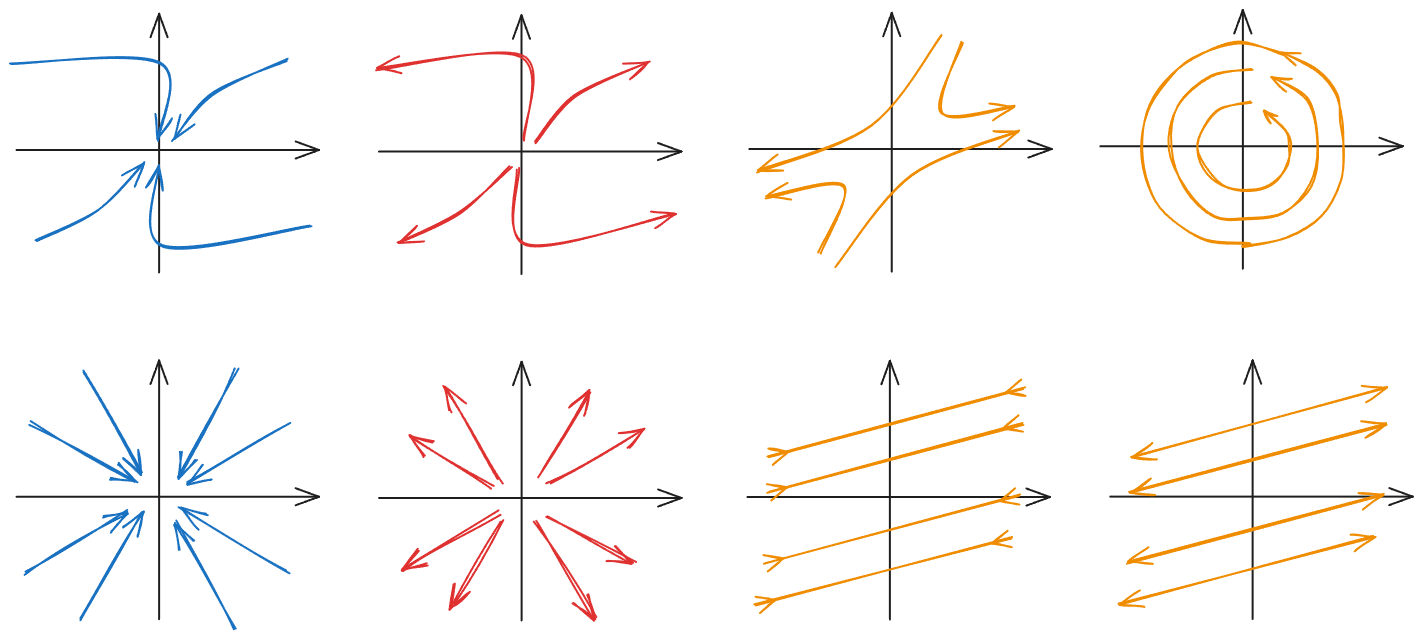
更高维的系统,连把 空间画清楚都不容易……
略微有些幽默的是,作为一个讨论时变函数的工具,相图中甚至(一般)不会出现时间。相图里的点,都是系统在某一时刻所可能处于的状态。从初始状态开始,按时间把系统经历的状态点连起来,就画出了动力学变量的轨迹。
一维:广义动量 vs. 广义坐标
因为这是一个一维动力学系统,纸面上还能余出一个维度让我们画出 :
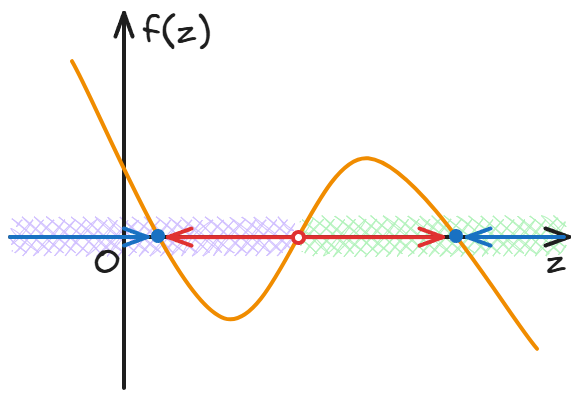
因为 f(z) 的意义是 z 的变化率,或者说“广义速度”,上图中 f(z) 在零轴以上时的 z,在下一时刻取值都会增加,也就是向右移动;f(z) 低于零轴处的 z 会向左移动。于是图中的红色空心圆点把 z 轴分成了两个区域 (domain),两个区域中的点在足够长的时间之后会收敛到各自内部的蓝色实心圆点。
驻点 (fixed point)
驻点 z* 就是动力学系统中的各个物理量一旦到达,就不再随时间变化的取值。
一维动力学系统 的驻点 ,就是函数 f 的零点。
前面的相图里,蓝色的两个实心点和红色的空心点都是驻点。
讨论驻点对动力学研究的意义,应该比较显然:
- 现今正在发展演化的动力学系统,我们希望知道它将往何处去;
- 现今已经静止的系统,物理量的取值往往是以前的动力学系统演化到时间 后收敛的结果,(在误差范围内)也就是旧系统的稳定驻点。
而在高维动力学系统中,因为维度的提高,会引入和驻点相关的更多概念,例如鞍点 (saddle point)、零斜率线 (nullcline)、极限环 (limit cycle)、吸引子 (attractor)、奇异吸引子 (exotic attractor)……
稳定性 (stability)
前文的“稳定”驻点,未加解释地使用了稳定性的概念——
所谓稳定性所刻画的性质是,当物理量位于驻点的邻域时,之后的时间里会渐进还是远离驻点。
也就是令 , 判断 的正负,往往需要将 f 在驻点附近泰勒展开。
相图里,习惯上用实心点表示稳定驻点,空心点表示不稳定驻点。
一维动力学系统 在驻点 的稳定性,一般情况看函数 f 在 处的导数,一阶为 0 时还要看高阶,但总而言之,f 从左上到右下穿越横轴则驻点稳定,左下到右上穿越零轴则不稳定,碰到零轴弹回原来的半平面则为半稳定。
科学之所以不害怕误差,除了之前文章里提到的成体系的误差分析工具之外,还因为绝大多数物理量都是动力学系统的稳定驻点,只要理论没失效,即便当前理论预测和测量值有差距,这种差距也至少不会随着时间推移而越差越远。
“物理图像”
此处讨论的空间是相空间 (phase space),也就是动力学变量张成的数学上的空间,而不再是普通人日常所说的那个现实物质所存在的空间。
对于物理专业的学生,往往在《理论力学》的学习中完成从位形空间到相空间的思维转变。转变之后不应该自满于“嘿嘿我说的话老百姓听不懂啦”的优越感,而要逆练神功,把相空间描述的物理在大脑中渲染回位形空间和时间,这也是保研夏令营面试题的主要出题思路。
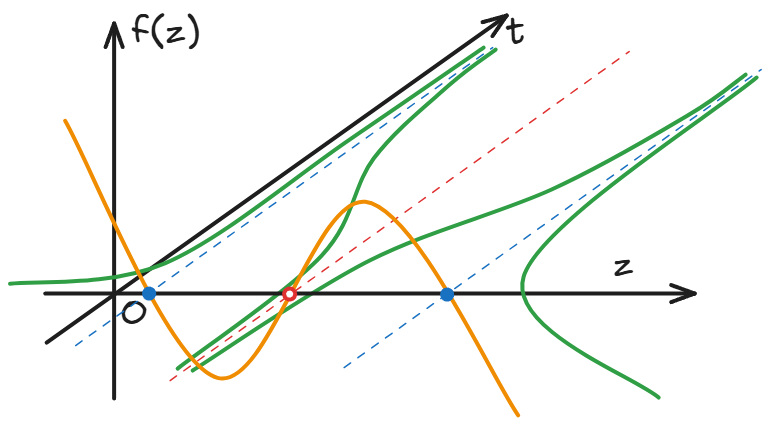
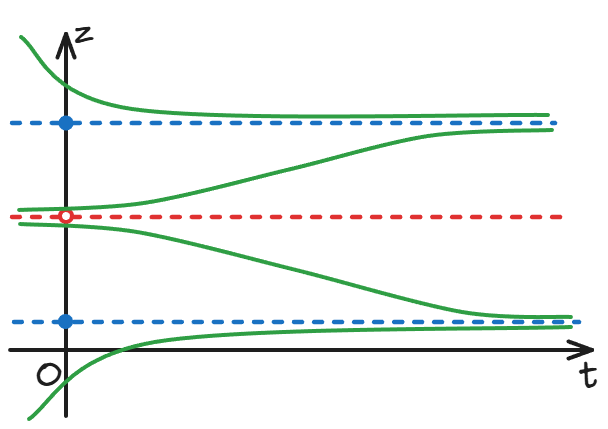
本文收录于以下合集: