.ai | PyTorch 中的自动微分 autograd

装了这么久的 ML/AI 爱好者，我发现我对 PyTorch 中的自动微分还是一知半解，停留在知道计算图和反向传播的概念，以及能看懂和小改别人写好的代码的水平。所以自觉还得再补补课。

~~真实动机是前女友找到了国内的研发工作，马上要回国赚大钱了，我破防了~~

之所以存在这样的认知断层，是因为介绍自动微分的时候一般是手动计算张量，然后给读者画个计算图；而真正干活的时候一般是写一个神经网络的类，这个类继承自 torch.nn.Module。

这样一包装，承载微分的张量很少被点名取用；而计算过程被一刀两段，绝大多数计算包装在了这个类的 forward() 方法中，但是最后一步计算模型预测和训练目标的差异 (loss)，往往留在了训练的控制流中，让人以为两者之间有什么本质区别。

其实不然——自动微分只针对 PyTorch 张量，torch.nn.Module 的实例是一个包含若干参数的函数，其参数要么是 torch.nn.Parameter，要么是其他含参的 torch.nn.Module 实例的参数，（用 .parameters() 方法取得，常见于 optimizer 的首个参数）。每次把训练输入张量带入这个函数，中间的数学计算就会被自动微分机制记录。对于自动微分来说，这些计算和最后对 loss 的计算没什么不同。

这个道理其实在做《一个 PyTorch 机器学习项目长什么样》这篇笔记的时候就应该理解，而实际上没有理解，说明——

一来信息和知识不是同一层面的概念，相同的信息嵌入在不同元信息中，可以给出不同深度的知识；

再者费曼学习法虽然像实验记录一样有让人快速恢复学习进度的好处，但也有让人沉溺于流量，忘记学习本心的危险，戒之在躁。

一个机器学习项目的过程包括：准备数据、定义模型、训练、评估效果。先来个简单例子：

import torch
from torch import data,nn,optim
# Data Preparation
dataset = data.Dataset(...)
trainloader = data.DataLoader(dataset,...)
# Model Definition
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # ...
    def forward(self, x):
        # forward calculation ...
        return x
net = Net()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
# Training
for epoch in range(2):
    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs
        inputs, labels = data
        # zero the parameter gradients
        optimizer.zero_grad()
        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        # print statistics
        # ...
print('Finished Training')
# Validation
correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)

张量——自动微分的对象

对于基本数据结构——张量，~~不应该~~ 也可以用大写的 torch.Tensor(data) 来创建；官方推荐的方法是小写的 torch.tensor(data)，产生的张量是 data 的拷贝，对一方的改动不反映到另一方。

如果数据已经是 numpy.ndarray 了，可以用 x_tensor = torch.from_numpy(x_array) 和 x_array = x_tensor.numpy() 互相转化，他们使用同一片内存，对一方的改动会反映到另一方。

更推荐的方法是用各种工厂函数，比如

torch.empty()
torch.zeros(), torch.zeros_like()
torch.ones(), torch.ones_like()
torch.eye()
torch.rand(), torch.rand_like()

其中在声明随机张量之前使用 torch.manual_seed(seed)，可以让距离该函数相同执行距离的随机数代码总是产生相同的数值：

https://pytorch.org/docs/stable/notes/randomness.html

尺寸相关

张量的尺寸是一个它本身的一个性质 x.shape, 属于 torch.Size 类。

张量之间的计算，在尺寸不同时，遵循类似 NumPy 的 broadcasting 规则。

x.item() 从一个单元素张量（不一定是标量）里取出它的值，返回值的数据类型不再是 PyTorch 自己的类型，而是 python 原生类型。

x.unsqueeze(dim) 在第 dim 个维度增加一个长度为 1 的维度。

更一般的改变形状需要 x.reshape(*new_shape) 和 torch.reshape(x,new_shape)

物理设备相关

一般数学函数也有 out 参数，可以原位写入已存在的张量，不改变原张量的 id。

原位计算是在一般数学函数名字后面加一下划线，如 torch.sin_(x), x1.add_(x2)

张量的赋值是传递指针，而不是传递数值。数值拷贝需要 x2 = x1.clone(). 克隆产物会保持和之前一样的 requires_grad 参数值。如果原张量在计算图里，新张量不需要的话应该 c = a.detach().clone()

参与运算的两个张量需要在同一设备 (CPU/GPU). 创建张量的时候可以用 device 参数声明设备，已经创建的张量可以用 x.to(device) 改变设备。

自动微分和神经网络相关

PyTorch 中的张量都有 requires_grad 参数，默认为 False。

对于带有 requires_grad=True 参数的张量，都受到自动微分机制 autograd 的控制。

前面每个每个创建张量的函数都接受这个参数，也自动传染给对自动微分的张量进行数学计算的结果。

神经网络，也就是继承自 torch.nn.Module 的对象（假设实例化为 net），内部有两个方法net.parameters() 和 net.buffers()，它们取到的是张量的 iterator，其中前者里面的张量（绝大多数）受 autograd 控制，后者不然。

要想取得某个神经网络的单个参数，需要知道 __init__() 方法中的变量名，以及官网文档中的参数名（一般在 Variables 小节，比如这个例子）

class MyNetwork(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.param1 = torch.nn.Parameter(torch.zeros((5,)),requires_grad=True)
        self.linear = torch.nn.Linear(in_features=5,out_features=1,bias=True)
    def forward(self,x):
        return self.linear(x * self.param1)
net = MyNetwork()
with torch.no_grad():
    print(net.param1)
    print(net.linear.weight)
    print(net.linear.bias)

自动微分

autograd 自动根据代码动态构建计算图：

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
b = torch.sin(a)
c = 2 * b
d = c + 1
out = d.sum()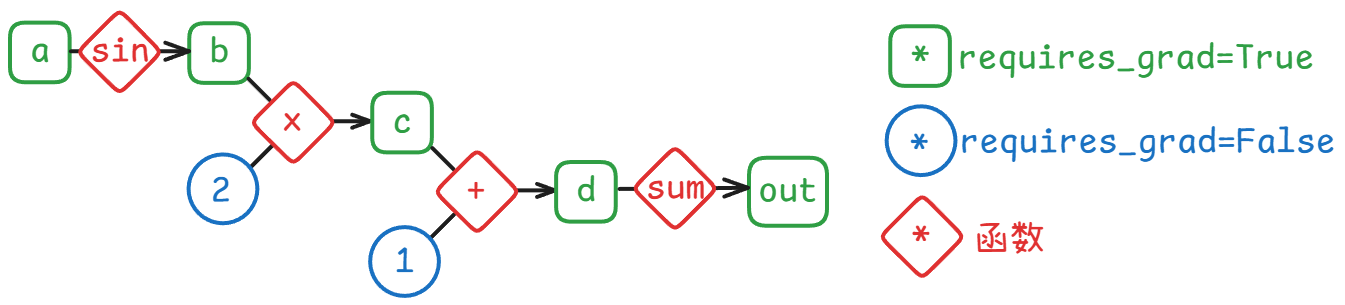

对于数学函数 b = f(a,*args) 计算出来的张量 b ——

`.grad_fn` 是一个函数

输入只有一个，尺寸需要和 a 的尺寸对齐 ~~（我感觉很奇怪）~~
输出的数量等于计算出这个张量的函数的输入的数量。
~~直接运行这个函数，基本就是把输入张量重复输出~~。从这个问答来看，直接运行这个函数几乎没有意义，因为自动微分是用其他编程语言实现的，SinBackward0 并不是 Python 对象。
t.grad_fn.next_functions 是一个 tuple，成员是 x1 等参数的 .grad_fn, 可以继续递推到工厂函数创建的张量，也就是这个计算图的叶节点。叶节点的 .grad_fn 为 None

print(a.grad_fn)   # None
print(b.grad_fn)   # <SinBackward0 object at 0x000001C8E240F400>
print(c.grad_fn)   # <MulBackward0 object at 0x000001C8E240EB30>
print(d.grad_fn)   # <AddBackward0 object at 0x000001C8E240F400>
print(out.grad_fn) # <SumBackward0 object at 0x000001C8E240F190>

`.backward()`

默认状态下，计算图的最终节点 out 是一个标量，也就是 0 阶张量。
- 要想让计算图的最终节点是一个高阶张量，需要指定 out.backward(gradient) 参数。gradient和 out 尺寸相同，两者对应元素相乘后求和，从而成为一个标量。
- 这种设定可以让一个张量的梯度 .grad 的尺寸只和自身的尺寸相等；如果允许计算从 out 到自身的 Jacobian 矩阵，会导致计算规模按多项式（一般是平方）增长。
默认状态下，一个计算图只能有一个.backward()，且只能执行一次。多次执行会报 RuntimeError: “Trying to backward through the graph a second time”。
- 要想对完全相同的计算图做多次 .backward(), 需指定 out.backward(retain_graph-True) 参数。

`t.grad`

偏导数张量 $\partial\mathrm {out}/\partial \mathrm t$ ，在最终节点运行 .backward() 之后，计算图中各节点的 .grad 会自动被 autograd 赋值
默认情况下，只有计算图的叶节点可以访问其 .grad
要取得中间节点的 .grad，需要在 .backward() 之前对相应张量执行 .retain_grad()

b.retain_grad()
out.backward()

print(a.grad)   # tensor([...],...), 约等于 2 * torch.cos(a)
print(b.grad)   # tensor([2.,2.,2.,...2.],...)
print(c.grad)   # None，不是计算图的叶节点，也没有 .retain_grad()
print(d.grad)   # None，不是计算图的叶节点，也没有 .retain_grad()
print(out.grad) # None，不是计算图的叶节点，也没有 .retain_grad()

以上各个操作基本上符合数学的习惯。

张量及其微分的更新

以下设定更多的是为了工程上方便：

.grad 是一个张量的性质，不是最终节点和该张量两者之间的性质，也不是计算图整体的性质。

不论是 .backward(retain_graph=True)，还是另外构建了新的计算图并运行 .backward()（比如训练时加载了训练集的新一轮 batch），当一个已有 .grad 的张量被新的 .backward() 波及时，.grad 的新值会是旧值和本轮偏导数的相加。

如果不想要这种累加，需要主动提前将张量 .grad 改成 0 或者 None。

除了梯度张量的置 0，

手动

正常情况下，requires_grad=True 的张量，对其做的所有操作都会被 autograd 记录，包括赋值操作，这就导致正常情况下，不论是清空梯度，还是根据梯度更新模型的参数，会导致 auto grad 的混乱。

所以需要特殊操作，通知 autograd 某些对受控张量的改动，不需要成为计算图的一部分。

所谓的特殊操作就是 torch.no_grad()

a = torch.arange(5.,requires_grad=True)
b = torch.sin(a)
b.backward(gradient=torch.ones_like(b))
with torch.no_grad():
    a[1] = 10
    a.grad.zero_()  # a.grad = 0
print(a)  # tensor([0,10,2,3,4], requires_grad=True)

在完全不涉及训练，只需要推理的环境，with torch.inference(): 比 with torch.no_grad(): 更节省计算资源。

自动

PyTorch 提供了上述操作的接口。

神经网络的参数的更新有一整个 torch.optim 模块提供的更新参数的方式（Optimizer 的子类）。里面的优化器都实现了两个方法：.step() 和 .zero_grad()，前者修改参数本身的值，后者将各参数的梯度归零。

class MyModel(torch.nn.Module):
    def __init__():
        # ...
    def forward(x):
        # ...
        return x
net = MyModel()
opt = torch.optim.SGD(net.parameters(),lr=0.01)
for e in range(epoch):
    # ...
    opt.step()
    opt.zero_grad()

如果只需要将梯度归零的话，nn.Module 也有一个 .zero_grad() 方法。

`tensor` vs. `tensor.data`

看 SGD 优化器的源码的时候，看到更新权重的时候不是 with torch.no_grad():，而是用到了张量的 a.data 和 a.grad.data

a vs. a.data, b.grad vs. b.grad.data 的区别今天不需要知道，不应该知道。这是旧的 Variable 对象的残留，新的接口将 Variable 合并进了 Tensor，.data 只是为了兼容旧代码而存在的，不再推荐这种用法。

本文收录于以下合集：

2024 年 11 月 10 日.ai | PyTorch 中的自动微分 autogradmdpyai

.ai | PyTorch 中的自动微分 autograd

目录

张量——自动微分的对象

自动微分

张量及其微分的更新

张量——自动微分的对象

尺寸相关

物理设备相关

自动微分和神经网络相关

自动微分

.grad_fn 是一个函数

.backward()

t.grad

张量及其微分的更新

手动

自动

tensor vs. tensor.data

.pyPython 学习笔记

.mdIT类业余笔记

.ai机器学习和人工智能

`.grad_fn` 是一个函数

`.backward()`

`t.grad`

`tensor` vs. `tensor.data`