本文是《Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next》这篇综述的读书笔记。
本文是《Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next》这篇综述的读书笔记。
年前,今年新入职的天文学方面的一位老师给我们群发邮件,宣传某国家实验室超算的 GPU 编程马拉松活动,他可以担任指导老师。于是毫不意外地,我报了名。该编程马拉松项目还需要专门申请,申请材料里要写清楚打算干什么,于是报名的五六个人七嘴八舌地想创意。基于物理的神经网络 PINN 就是天文老师的点子。
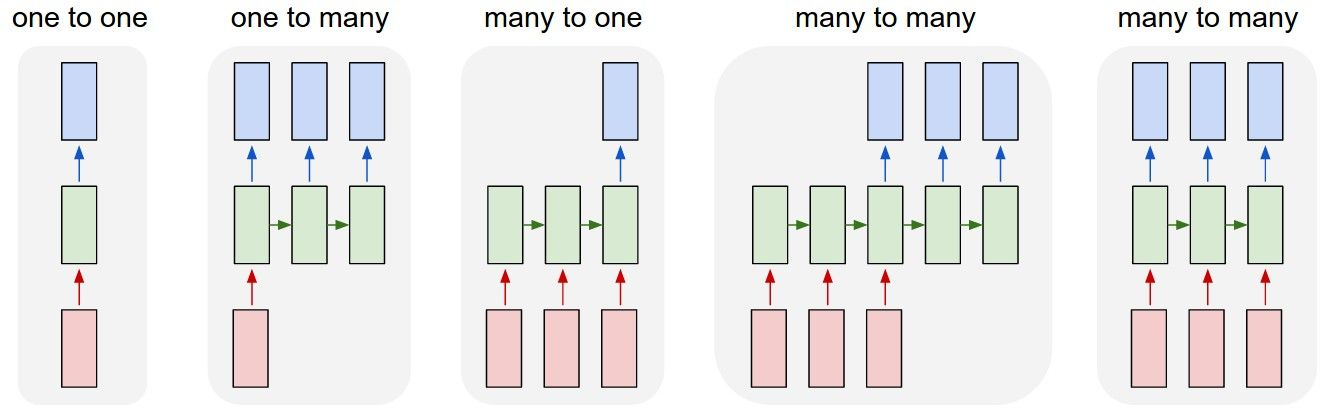
~~写到这里,我才意识到,老哥是不是想拿我们当免费劳动力啊~~~
神经网络可以看作是一个复杂的非线性函数,接受一个(一般来说维度很高的)向量作为输入,一番计算后输出另一个向量。训练神经网络,就是找到这个函数的参数,绝大多数找参数的方法涉及计算网络输出对参数的偏导数,因此神经网络计算框架的核心功能就是自动微分 (auto-differentiation)。
而很多物理问题,都可以用(偏)微分方程来描述,微分方程的解不是变量,而是函数,而且往往是复杂的非线性函数。所以基于物理的神经网络 (PINN) 就是以神经网络来表达这个函数,然后把这个函数带入到物理的微分方程中,把神经网络输出和真正的物理解之间的差距当作损失函数,反向传播回去来优化神经网络的参数。代入方程时的微分计算,正好可以利用现成框架的自动微分功能。
在以 GPT 为代表的 transformer 类神经网络模型出现之前,自然语言处理类的机器学习项目,往往要在网络之外,利用人类的语法知识,对语段进行语义分割等等“中间任务”。Transformer 一出,算力出奇迹,中间任务逐渐变得没有必要了。
在 GPT 崭露头角,并且越来越有迹象表明其将会涌现出通用人工智能的今天,这些基于物理的神经网络,会不会还未成熟就已过时?这种心情,就和《三体》第二卷开始,章北海和吴岳面对焊渍未漆的“唐”号航空母舰时差不多吧……
- Abstract
- PINNs are neural networks that encode model equations. a NN must fit observed data while reducing a PDE residual.
-
Introduction
-
The “curse of dimensionality” was first described by Bellman in the context of optimal control problems. (Bellman R.: Dynamic Programming. Sci. 153(3731), 34-37 (1966))
-
Early work: MLP (multilayer perceptron) with few hidden layers to solve PDEs. (https://doi.org/10.1109/72.712178)
-
感觉可能更全面的一篇综述:https://doi.org/10.1007/s12206-021-0342-5。该文关注 what deep NN is used, how physical knowledge is represented, how physical information is integrated,本文只关于 PINN, a 2017 framework。
- What the PINNs are
- PINNs solve problems involving PDEs:
- approximates PDE solutions by training a NN to minimize a loss function
- includes terms reflecting the initial and boundary conditions
- and PDE residual at selected points in the domain (called collocation points)
- given an input point in the integration domain, returns an estimated solution at that point.
- incorporates a residual network that encodes the governing physical equations
- can be thought of as an unsupervised strategy when they are trained solely with physical equations in forward problems, but supervised learning when some properties are derived from data
- Advantages:
- mesh-free? 但是我们给模型喂训练数据的时候往往已经暗含了 mesh 了吧
- on-demand computation after training
- forward and inverse problem using the same optimization, with minimal modification
- PINNs solve problems involving PDEs:
- What this Review is About
- 提到了一个做综述找文章的方法:本文涉及的文章可以在 Scopus 上进行高级搜索:
((physic* OR physical)) W/2 (informed OR constrained) W/2 “neural network”)
- 提到了一个做综述找文章的方法:本文涉及的文章可以在 Scopus 上进行高级搜索:
-
-
The Building Blocks of a PINN
- question:
- solution:
- Neural Network Architecture
-
DNN (deep neural network) is an artificial neural network that is deeper than 2 layers.
- Feed-Forward Neural Network:
-
-
Just change CNN from convolution to fully connected.
-
Also known as multi-layer perceptrons (MLP)
- FFNN architectures
- Tartakovsky et al used 3 hidden layers, 50 units per layer, and a hyperbolic tangent activation function. Other people use different numbers but of the same order of magnitude.
- A comparison paper: Blechschmidt, J., Ernst, O.G.: Three ways to solve partial differential equations with neural networks –A review. GAMM-Mitteilungen 44(2), e202100,006 (2021).
- multiple FFNN: 2 phase Stephan problem.
- shallow networks: for training costs
- activation function: the swish function in the paper has a learnable parameter, so — how to add a learnable parameter in PyTorch
-
- Convolutional Neural Networks:
-
I am most familiar with this one.
-
-
performs well with multidimensional data such as images and speeches
- CNN architectures:
PhyGeoNet: a physics-informed geometry-adaptive convolutional neural network. It uses a coordinate transformation to convert solution fields from irregular physical domains to rectangular reference domains.- According to Fang (https://doi.org/10.1109/TNNLS.2021.3070878), a Laplacian operator can be discretized using the finite volume approach, and the procedures are equivalent to convolution. Padding data can serve as boundary conditions.
- convolutional encoder-decoder network
-
- Recurrent Neural Network
-
, where f is the layer-wise function, x is the input, h is the hidden vector state, W is a hidden-to-hidden weight matrix, U is an input-to-hidden matrix and b is a bias vector. 我认为等号左边的 应当作为下标
-
感觉有点像 hidden Markov model,只不过 Markov 中间的 hidden layers 好像与序号无关(记不清了),
RNN 看起来各个 W 和 H 似乎不同。RNN cell is actually the exact same one and reused throughout. (from https://blog.floydhub.com/a-beginners-guide-on-recurrent-neural-networks-with-pytorch/). Cartoon from Wikipedia: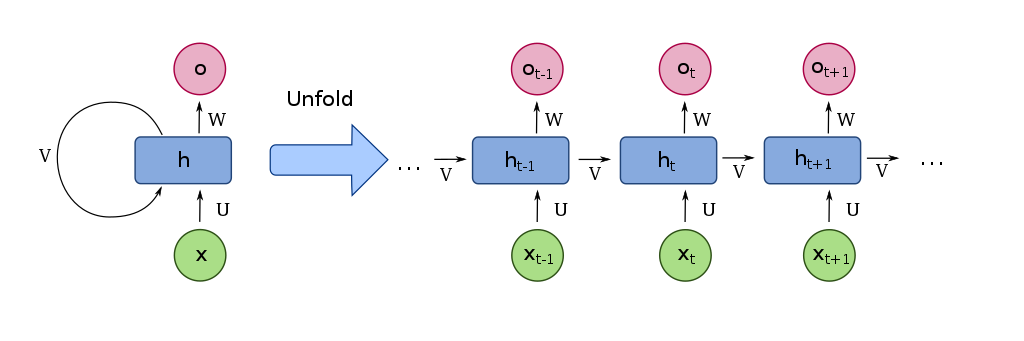
-
From https://blog.floydhub.com/a-beginners-guide-on-recurrent-neural-networks-with-pytorch/:

- RNN architectures
- can be used to perform numerical Euler integration
- 基本上输出的第 i 项只与输入的第 i 和 i-1 项相关。
- LSTM architectures
- 比 RNN 多更多中间隐变量,至于怎么做到整合长期记忆的,技术细节现在可以先略过
-
- other architectures for PINN
- Bayesian neural network: weights are distributions rather than deterministic values, and these distributions are learned using Bayesian inference. 只介绍了一篇文章
- GAN architectures:
- two neural networks compete in a zero-sum game to deceive each other
- physics-informed GAN uses automatic differentiation to embed the governing physical laws in stochastic differential equations. The discriminator in PI–GAN is represented by a basic FFNN, while the generators are a combination of FFNNs and a NN induced by the SDE
- multiple PINNs
-
- Injection of Physical Laws
- 既然是要解常/偏微分方程,那么微分计算必不可少。四种方法:hand-coded, symbolic, numerical, auto-differentiation,最后一种显著胜出。所谓 auto-differentiation, 就是利用现成框架,框架自动给出原函数的导数的算法。
- Differential equation residual:
- : 原文给出了来源,但是从字面上看不出来与前式的等价性
- Boundary condition residual:
- Model Estimation by Learning Approaches
- Observations about the Loss
- accounts for the fidelity of the PDE model. Setting it to 0 trains the network without knowledge of underlying physics.
- In general, the number of is more than the measurements, so regularization is needed.
- The number and position of residual points matter a lot.
- Soft and Hard Constraints
- Soft: penalty terms. Bad:
- satisfying BC is not guaranteed
- assignment of the weight of BC affects learning efficiency, no theory for this.
- Hard: encoded into the network design. Zhu et. al
- Soft: penalty terms. Bad:
- Optimization methods
- minibatch sampling using the Adam algorithm
- increased sample size with L-BFGS (limited-memory Broyden-Fletcher-Goldfarb-Shanno)
- Observations about the Loss
- Learning theory of PINN: roughly in DE, consistency + stability → convergence
- convergence aspects: related to the number of parameters in NN
- statistical learning error analysis: use risk to define error
- Empirical risk:
- Risk of using approximator:
- Optimization error: the difference between the local and global minimum, is still an open question for PINN.
- Generalization error: error when applied to unseen data.
- Approximation error:
- Global error between trained deep NN and the correct solution is bounded:
- 有点乱,本来说 error 是误差,结果最后还是用 risk 作为误差
- error analysis results for PINN
-
Differential Problems Dealt with PINNs:读来感觉这一部分意义不大,将来遇到需要解决的问题时,回来看看之前有没有人做过就行了——另一方面看,一类方程就需要一类特殊构造的神经网络来解,那么说明神经网络解方程的通用性并不好~
- Ordinary differential equations:
- Neural ODE as learners, a continuous representation of ResNet. [Lai et al], into 2 parts: a physics-informed term and an unknown discrepancy
- LSTM [Zhang et al]
- Directed graph models to implement ODE, and Euler RNN for numerical integration
- Symplectic Taylor neural networks in Tong et al use symplectic integrators
- Partial differential equations: steady/unsteady的区别就是是否含时
- steady-state PDEs
- unsteady PDEs
- Advection-diffusion-reaction problems
- diffusion problems
- advection problems
- Flow problems
- Navier-Stokes equations
- hyperbolic equations
- quantum problems
- Advection-diffusion-reaction problems
- Other problems
- Differential equations of fractional order
- automatic differentiation not applicable to fractional order → L1 scheme
- numerical discretization for fractional operators
- separate network to represent each fractional order
- Uncertainty Estimation: Bayesian
- Differential equations of fractional order
- Solving a Differential Problem with PINN
- 1d non-linear Schrödinger equation
- dataset by simulation with MATLAB-based Chebfun open-source(?) software
- Ordinary differential equations:
-
PINNs: Data, Applications, and Software
- Data
- Applications
- Hemodynamics
- Flows Problems
- Optics and Electromagnetic Applications
- Molecular Dynamics and Materials-Related Applications
- Geoscience and Elastiostatic Problems
- Industrial Application
- Software
DeepXDE: initial library by one of the vanilla PINN authorsNeuroDiffEq: PyTorch based used at Harvard IACSModulus: previously known as Nvidia SimNetSciANN: implementation of PINN as Keras wrapperPyDENs: heat and wave equationsNeuralPDE.jl: part of SciMLADCME: extending TensorFlowNangs: stopped updates, but faster than PyDENsTensorDiffEq: TensorFlow for multi-worker distributed computingIDRLnet: a python toolbox inspired by Nvidia SimNetElvet: coupled ODEs or PDEs, and variational problems about the minimization of a functional- Other Packages
-
PINN Future Challenges and Directions
- Overcoming Theoretical Difficulties in PINN
- Improving Implementation Aspects in PINN
- PINN in the SciML Framework
- PINN in the AI Framework
-
Conclusion
本文收录于以下合集: