一个随机变量 X 取值为 x 的概率 (probability)/概率密度,一般可以用一个有若干参数的函数来表示。这个函数的参数记作 θ:
probX(x)=f(x∣θ)
而似然性 (likelihood) 就是把上式 f 看作以 θ 为自变量,x 为参数的函数,从表达式上看不出区别:
L(θ∣x)=f(x∣θ)=probX(x)
最近处理一个数据集,整理完之后的直方图如下:
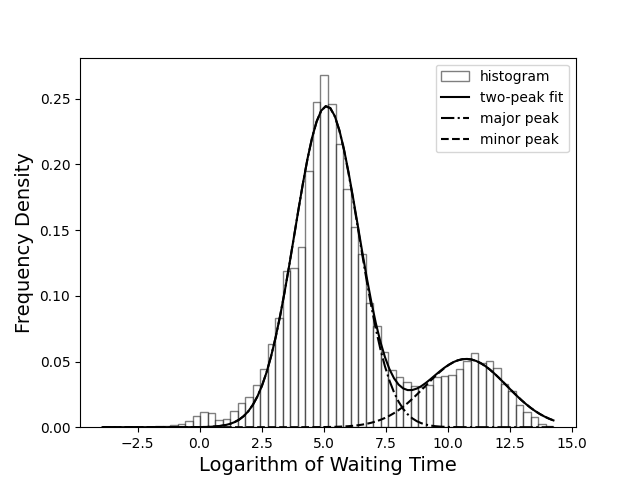 double-peak
double-peak
比较明显,比起一个正态分布 f(x)=σ2π1e−21(σx−μ)2,这些数据更像是来自不同均值和方差的两个分布。那么对于每个数据点 x0,它到底来自哪个分布呢?可以分别计算 L1(μ1,θ1∣x0)=f(x0∣μ1,θ1) 和 L2(μ2,θ2∣x0)=f(x0∣μ2,θ2),然后比较 L1 和 L2 的大小。