Dynamcis[3] | From Linear to Non-Linear Systems

In the previous post, I talked about the linear system $\dot{\vec z}=\mathrm d\vec z/\mathrm dt=\mathbb{\hat J}\cdot\vec z$, and introduced two concepts that seemed meaningless at the time:

• nullcline: fixed points are the intersections of zero-slope lines in all dimensions;
• Jacobian matrix: the generalized "slope" of generalized velocity in high-dimensional phase space.

Now consider the nonlinear system $\dot{\vec z}=\mathrm d\vec z/\mathrm dt=\vec f (\vec z)$. Its intuitive effects on the distortion of the linear system include:

• The zero slope line (if it exists) is no longer necessarily a straight line
  • The number of stationary points is no longer at most one;
  • The position of the stationary point (if it exists) is no longer fixed at the origin.
• The terms of the Jacobian matrix are no longer constants that are independent of z
  • The stability of the stationary point needs to be discussed separately according to the value of each stationary point z*.

Semi-quantitative Analysis Procedures

1. Nullclines
   1. Calculate $f_i=0$ and draw the zero slope line nullcline of each dimension;
   2. Along the zero slope line nullcline of each dimension, draw the magnitude and direction of the generalized velocity. The generalized velocity on the nullcline of the kth dimension is $(f_1,f_2,\dots,f_{k-1},0,f_{k+1},\dots)^T|_{nullcline}$
2. Fixed points
   1. Mark the intersection of the zero slope lines nullcline of all dimensions as stationary points
   2. Calculate the Jacobian matrix at the stationary point, and judge the type of stationary point by analogy with the linear system
3. Dynamic trajectories
   1. According to the type of stationary point and the generalized velocity on the zero slope line nullcline, interpolate and draw the generalized velocity at other positions
   2. Connect the generalized velocities from beginning to end into a dynamic trajectory

Example: a pendulum of a hard light stick

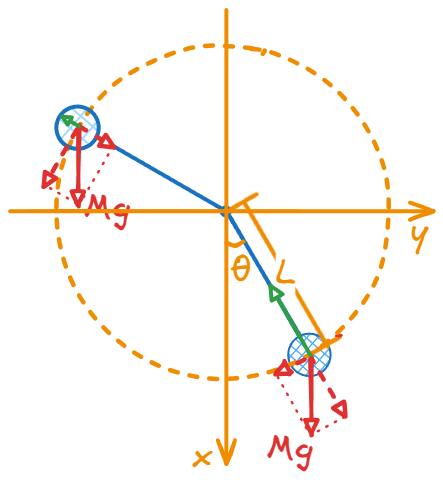
As shown in the picture,

• "Hard" means that the stick can exert force on the ball in both directions of extension and contraction, and the length of the stick remains unchanged;
• "Light" means that the entire mass of the pendulum is located on the ball;
• "Small" means that the ball can be regarded as a point mass;

In short, the places where we can argue are basically blocked~

There are 2 spatial dimensions in the diagram, 1 constraint on the length of the hard stick, so there is only 1 spatial degree of freedom. We take the free variable as the angle $\theta$ between the stick and the direction of gravity.

As mentioned in the 0th article of this series, Newton's second law is a second-order differential equation, so an intermediate variable is also needed, the angular velocity $\omega$.

The tangential acceleration is only provided by the tangential component of gravity, so

$$\begin{cases} \dot\theta = \mathrm d\theta/\mathrm dt = \omega \\ \dot\omega = \mathrm d\omega/dt=-g\sin\theta/L \end{cases}$$

The phase space is $(\theta,\omega)$

The nullcline in $\theta$ dimension is the $\theta$ axis, and the nullcline in $\omega$ dimension is the family of lines $\theta = n\pi,\ n=1,2,\dots$

The fixed points are $(n \pi, 0)^T,\ n=1,2,\dots$

The Jacobian matrix is $\left(\begin{matrix} 0 & 1 \\ -g\cos\theta/L & 0 \end{matrix}\right)$

When n is an even number, the eigenvalues ​​of the Jacobian matrix are $\pm i$, and the dynamical trajectory is closed around these fixed points;

For stationary points when n is an odd number, the eigenvalues ​​of the Jacobian matrix are $\pm 1$, and these fixed points are saddle points.

With interpolation, the phase portrait is as follows:

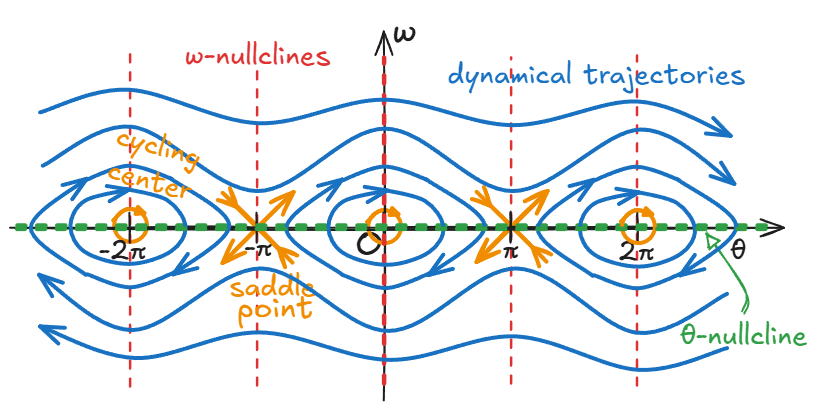
Rendering the physics described in phase space back into real space and time——

It can be seen that the system has translational symmetry in the $\theta$ direction and can be rolled into a vertical cylinder with a base circumference of $2\pi$, corresponding to the congruence equivalence class of angles.

It can be seen that the dynamic trajectories of the system can be divided into two categories:

• Closed loops between the saddle point and the center of the cycle: corresponds to the reciprocating swing that falls back when the mechanical energy is insufficient to reach the highest point;
• Infinitely extended curves away from the saddle point and the center of the cycle: corresponds to the rotation that continues forward after the mechanical energy is sufficient to break through the highest point.

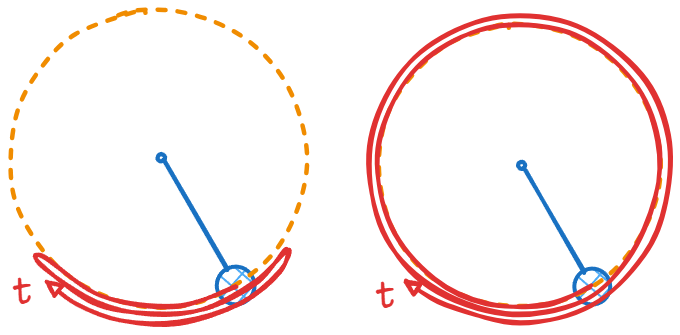
It can also be seen that the farther the dynamic trajectory is from the $\theta$ axis, the smaller the fluctuation in the $\omega$ direction. This is because the mechanical energy of all points on the same trajectory is equal. For the same pendulum, the gravitational potential energy depends on $\theta$ and is bounded, and the kinetic energy depends on $\omega$. Where the absolute value of $\omega$ is larger, the proportion of gravitational potential energy to mechanical energy is smaller, and its change has less obvious effect on the change of kinetic energy (angular velocity) required for the conservation of mechanical energy.

Fixed Points → Attractors/Repellers

As the dimension increases, the existence of stationary points, that is, the requirement that "the zero slope lines of all dimensions intersect at a certain point", becomes increasingly difficult to meet. At the same time, sometimes such strict conditions are not required, and the system will exhibit relatively stable behavior.

Therefore, the concept of stable stationary points is relaxed to attractors, which are subsets of phase space that satisfy the following three conditions:

1. Invariant: The system whose initial value is inside the attractor will also have its trajectory inside the attractor in the subsequent time periods.
2. Attractive: The system whose initial value is outside the attractor will be attracted to the vicinity after time evolution.
3. Minimal: There is no subset inside the attractor that satisfies the first two conditions.

The fixed line of the linear system mentioned above meets the definition of an attractor if it is stable.

Also analogous to the unstable fixed point, the opposite structure of attractor in phase space is called a repeller.

Limit cycle

A stable limit cycle is a type of attractor.

An unstable limit cycle is a type of repeller.

The example we used in class was a dynamic system in polar coordinates:

$$\begin{cases} \dot r = \mathrm dr/\mathrm dt = r+r^3-r^5\\ \dot \theta = \omega+br^2 \end{cases}$$

The angular velocity increases the farther away from the origin, which is meaningless;

There are two stable stationary points and one unstable stationary point in terms of radius:

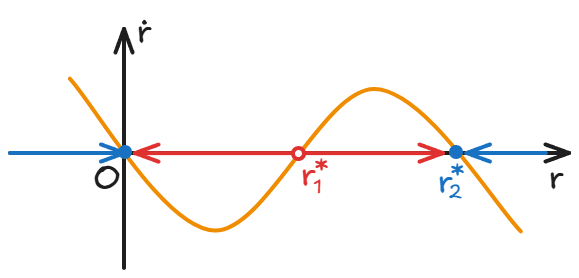
And when we use Cartesian coordinates to represent this system:

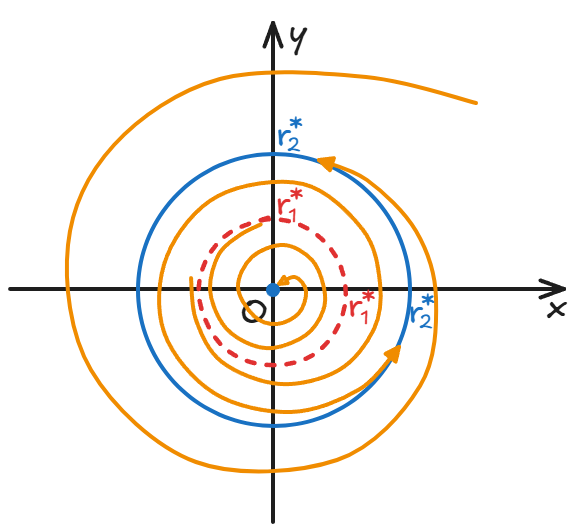
The circle with a radius of $r_2^*$ satisfies the definition of attractor above. Trajectories with an initial radius greater than $r_1^*$ will tend to move in a circle around the blue circle after a long enough time.

The circle with $r_1^*$ as radius satisfies our definition of repeller above. Trajectories with an initial radius smaller than $r_2^*$ will tend to spiral away from the red circle after a long enough time.

Both circles are limit cycles.

What's next

Chaos and its implication in truthness and freedom.