因为高维空间难以靠直觉理解（冯 ·诺伊曼和他妹妹：我们不觉得），所以高维动力学一般先讨论线性系统，然后把非线性的效果当成对线性系统的扭曲。

A tentative English translation, not rigorously proof-read yet.

n 维的线性动力学系统，写成矩阵乘法形式：

(z˙1z˙2⋮z˙n)=ddt(z1z2⋮zn)=(J11J12…J1nJ21J22…J2n⋮⋮⋱⋮Jn1Jn2…Jnn)(z1z2⋮zn)\left(\begin{matrix} \dot z_1\\\dot z_2\\\vdots\\\dot z_n\end{matrix}\right)=\frac{\mathrm d}{\mathrm dt}\left(\begin{matrix}z_1\\z_2\\\vdots\\z_n\end{matrix}\right)=\left(\begin{matrix} J_{11} & J_{12} & \dots & J_{1n} \\ J_{21} & J_{22} & \dots & J_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ J_{n1} & J_{n2} & \dots & J_{nn} \\ \end{matrix}\right) \left(\begin{matrix}z_1\\z_2\\\vdots\\z_n\end{matrix}\right)

这个常微分方程组 dz⃗/dt=J^⋅z⃗\mathrm d\vec z/\mathrm dt=\hat J\cdot\vec z 可以直接求解.

线性微分方程通解

J^\hat J 一般是一个实矩阵，令 λi\lambda_i 和 v⃗i\vec v_i 是矩阵 J^\hat J 的本征值和本征向量，

在各个本征值互不相等的情况下

z⃗=∑incieλitv⃗i=c1eλ1tv⃗1+c2eλ2tv⃗2+⋯+cneλntv⃗n\vec z = \sum_i^n{c_ie^{\lambda_it}\vec v_i} = c_1e^{\lambda_1t}\vec v_1 + c_2e^{\lambda_2t}\vec v_2+\dots+c_ne^{\lambda_nt}\vec v_n

其中 cic_i 是初值条件确定的常数，各本征向量 v⃗i\vec v_i 之间不一定正交。

其中某一本征值 λi\lambda_i 可能是正数、负数、复数、0、与其他本征值重合。经过足够长时间的演化——

  • 正数：z⃗\vec z 各分量沿 v⃗i\vec v_i 方向发散到无穷；
  • 负数：z⃗\vec z 各分量量沿 v⃗i\vec v_i 方向收敛到原点；
  • 0：z⃗\vec z 各分量在 v⃗i\vec v_i 方向上没有变化，v⃗i\vec v_i 表示的过原点的直线成为系统的“驻线”
  • 复数：λ\lambda 及其共轭 λ∗\lambda^* 都是 J^\hat J 的本征值，各变量在这对本征向量之间根据欧拉公式螺旋，实部为正则往无穷远处螺旋，为负则往原点螺旋；
  • 与其他本征值相等，令该本征值的重数为 k，则方程的解变为 z⃗=∑in−kcieλitv⃗i+∑jkdjtj−1v⃗\vec z = \sum_i^{n-k}{c_ie^{\lambda_it}\vec v_i}+\sum_j^kd_jt^{j-1}\vec v

当各本征值不为零时，线性系统最多只有一个驻点，也就是原点。

以二维线性系统为例

在 2 维时， J^\hat J 矩阵的本征值由矩阵的迹 Tr[J^]\mathrm{Tr}[\hat J] 和行列式 Det[J^]\mathrm{Det}[\hat J] 给出

λ±=Tr[J^]±Tr2[J^]−4 Det[J^]2\lambda_{\pm}=\frac{\mathrm{Tr}[\hat J]\pm\sqrt{\mathrm{Tr}^2[\hat J]-4\ \mathrm{Det}[\hat J]}}{2}

系统的相图——

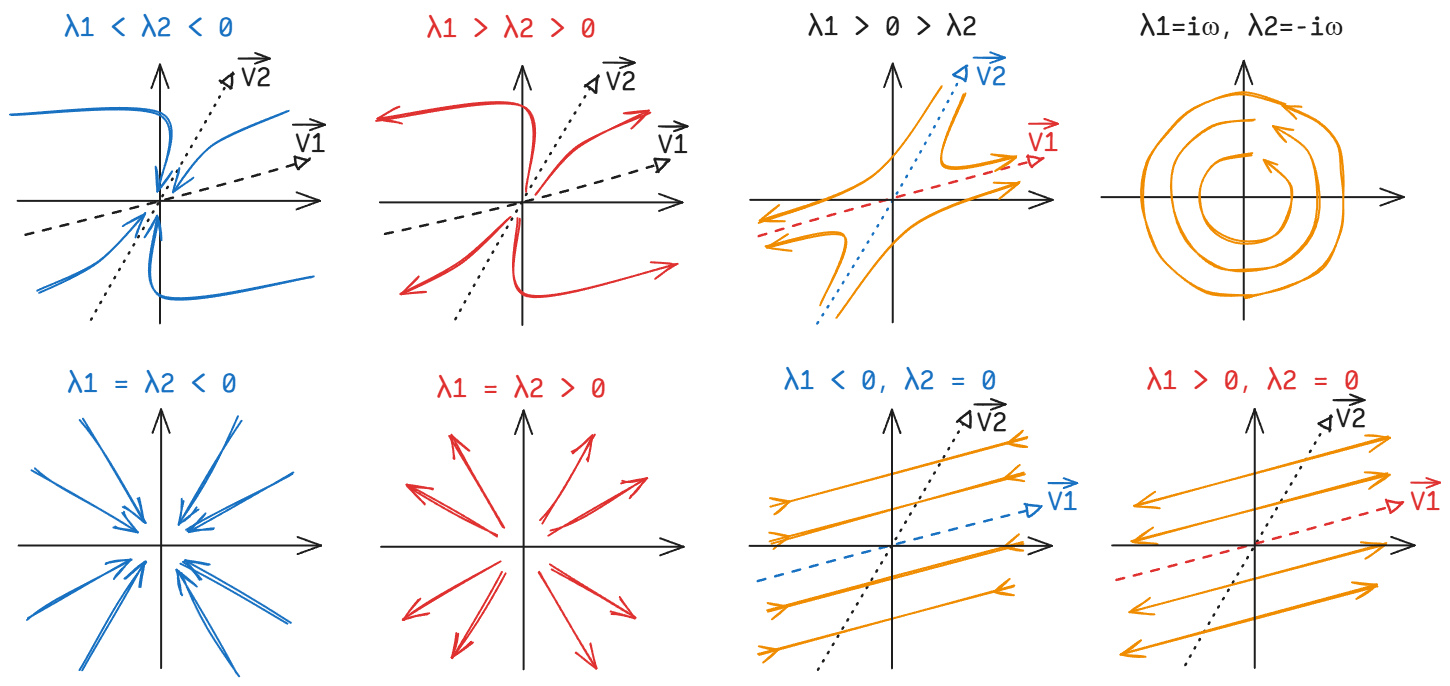
距离原点无限远处，动力学轨迹的切线趋近于本征值的绝对值较大的那个本征向量。

可以看到除了稳定和不稳定驻点（左侧 4 图），二维系统比一维多出好几种情况（右侧 4 图）。

  • 两个本征值一正一负时的驻点叫做鞍点 (saddle point)。
  • 其中一个本征值为 0 时， 对应的本征向量表示的过原点直线是系统的驻线 (fixed line)
  • 两对本征值为共轭复数时，系统会有周期现象，但要到非线性系统中才会出现极限环 (limit cycle)

零斜率线

一维系统只有一个 f 函数，求解驻点也就只需要算这一个函数的零点。

高维动力学中，每一个维度的 fif_i 都可以求零点，解是一个 n-1 维的几何结构，名为 nullcline。在二维动力学系统中，nullclines 是一维结构，也就是直线/曲线。

在第 k 个维度的 nullcline 上，变量 zkz_k 的变化率为 0，相空间中广义坐标的轨迹的切线和 zkz_k 的数轴正交。

而驻点就是所有 n 个 nullclines 共同的交点。

雅各比矩阵

矩阵形式表示的线性系统，J^\hat J 的第 i 行第 j 列正好是 ∂z˙i/∂zj=∂fi/∂zj\partial\dot z_i/\partial z_j = \partial f_i/\partial z_j，这种两个向量之间的偏导数矩阵，叫做雅各比 (Jacobian) 矩阵 J\mathbb J。

线性系统的雅各比矩阵，各元素是与 ziz_i 无关的常数。

非线性系统的雅各比矩阵，各元素一般是以 ziz_i 为变量的表达式。

雅各比矩阵被用来讨论驻点/吸引子的稳定性，在下一章非线性系统中的作用更加明显。

下集预告

非线性系统的定性和半定量分析框架

本文收录于以下合集：