非线性动力学系统和线性系统的不同；半定量分析流程；吸引子

    A tentative English translation, not rigorously proof-read yet.

    上回书说了线性系统 z⃗˙=dz⃗/dt=J^⋅z⃗\dot{\vec z}=\mathrm d\vec z/\mathrm dt=\mathbb{\hat J}\cdot\vec z，引入了两个当时看起来没什么意思的概念：

    • 零斜率线 (nullcline)：驻点是所有维度的零斜率线的交点；
    • 雅各比 (Jacobian) 矩阵：高维相空间中广义速度的广义“斜率”。

    现在来考虑非线性 z⃗˙=dz⃗/dt=f⃗(z⃗)\dot{\vec z}=\mathrm d\vec z/\mathrm dt=\vec f (\vec z)，它对线性系统扭曲的直观效果包括：

    • 零斜率线（如果存在）不再一定是直线
      • 驻点的数量不再最多只有一个；
      • 驻点的位置（如果存在）不再固定位于坐标原点。
    • 雅各比矩阵的各项不再是与 z 无关的常数
      • 驻点的稳定性需要根据各个驻点 z* 的值分别讨论。

    半定量分析流程

    1. 零斜率线
      1. 计算 fi=0f_i=0 并画出各个维度的零斜率线 nullcline；
      2. 沿着每个维度的零斜率线 nullcline，画出广义速度的大小和方向，第 k 个维度的 nullcline 上的广义速度为 (f1,f2,…,fk−1,0,fk+1,… )T∣nullcline(f_1,f_2,\dots,f_{k-1},0,f_{k+1},\dots)^T|_{nullcline}
    2. 驻点
      1. 将所有维度的零斜率线 nullcline 的交点标记为驻点
      2. 计算驻点处的雅各比矩阵，类比线性系统，判断驻点的类型
    3. 动力学轨迹
      1. 根据驻点类型，也根据零斜率线 nullcline 上的广义速度，插值画出其他位置上的广义速度
      2. 将首尾相接的广义速度连缀成动力学轨迹

    举个例子：没有小角近似的硬轻棍摆

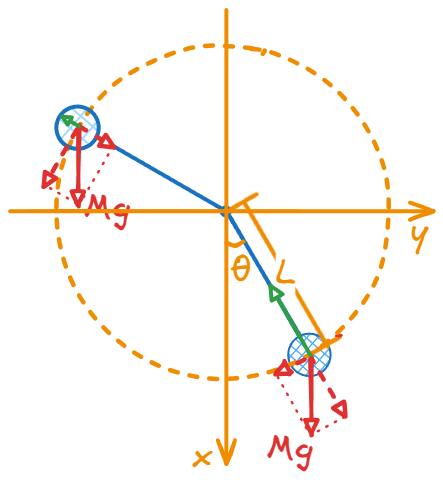
    物理摆的受力分析
    物理摆的受力分析

    如题也如图所示，“硬”的意思是棍可以在伸缩两个方向上对小球施力，且棍的长度不变；“轻”的意思是摆的全部质量位于小球上；“小”的意思是球可以看作质点；总之，能抬杠的地方基本上都堵死了～

    图中有 2 个空间维度，1 个硬棍长度的约束，所以只有 1 个空间自由度。我们取自由变量为棍与重力方向的夹角 θ\theta。

    如本系列第 0 篇所说，牛顿第二定律是一个二阶微分方程，所以还需要一个中间变量，角速度 ω\omega。

    切向加速度只由重力的切向分量提供，所以

    {θ˙=dθ/dt=ωω˙=dω/dt=−gsin⁡θ/L\begin{cases} \dot\theta = \mathrm d\theta/\mathrm dt = \omega \\ \dot\omega = \mathrm d\omega/dt=-g\sin\theta/L \end{cases}

    相空间是 (θ,ω)(\theta,\omega)

    θ\theta 维度的零斜率线就是 θ\theta 轴，ω\omega 维度的零斜率线是 θ=nπ, n=1,2,…\theta = n\pi,\ n=1,2,\dots 的直线族

    系统的驻点是 (nπ,0)T, n=1,2,…(n \pi, 0)^T,\ n=1,2,\dots

    雅各比矩阵是 (01−gcos⁡θ/L0)\left(\begin{matrix} 0 & 1 \\ -g\cos\theta/L & 0 \end{matrix}\right)

    n 为偶数时的驻点，雅各比矩阵的本征值是 ±i\pm i，动力学轨迹绕这些驻点闭环；

    n 为奇数时的驻点，雅各比矩阵的本征值是 ±1\pm 1，这些驻点是鞍点。

    经过亿点插值，画出的相图：

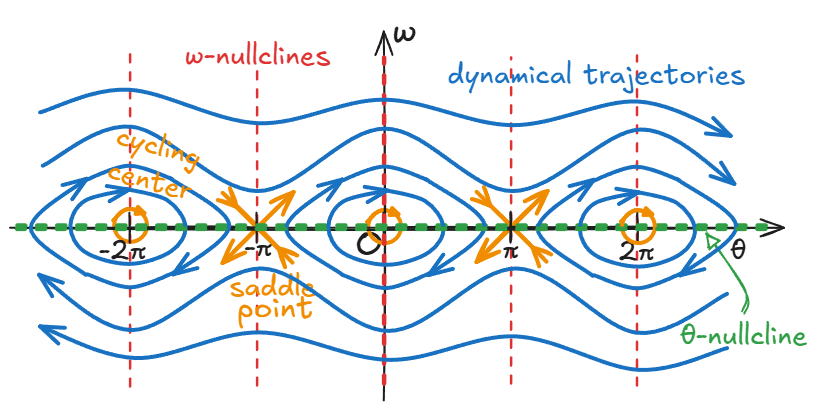
    物理摆的相图 (phase portrait)
    物理摆的相图 (phase portrait)

    本系列第 1 篇说过，完成从位形空间到相空间的思维转变之后，不应该自满于“嘿嘿我说的话老百姓听不懂啦”的优越感，而要逆练神功，把相空间描述的物理在大脑中渲染回位形空间和时间——

    可以看到，系统在 θ\theta 方向具有平移对称性，可以卷成一个底面周长为 2π2\pi 的竖直圆筒，对应于角度的同余等价类。

    又可以看到，系统的动力学轨迹可以分为两类：

    • 夹在鞍点和循环中心之间的，闭合环路：对应于机械能不足以到达最高点就落回去的往复摆动；
    • 远离鞍点和循环中心的，无限延展曲线：对应于机械能足以冲过最高点之后继续向前的转动。
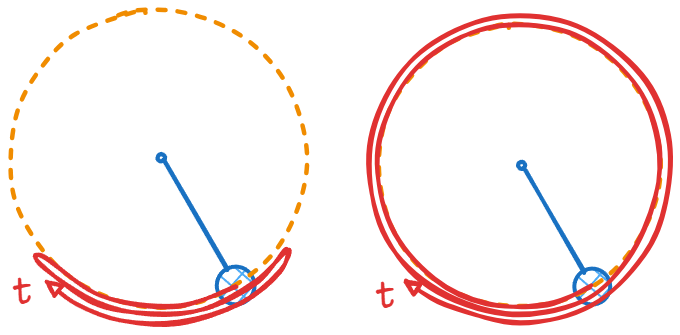
    系统的相空间轨迹可以分为两类
    系统的相空间轨迹可以分为两类

    还可以看到，距离 θ\theta 轴越远的动力学轨迹，ω\omega 方向上的涨落越小。这是因为同一轨迹上所有点的机械能相等，对于同一个摆，重力势能取决于 θ\theta 且有界，动能取决于 ω\omega。ω\omega 绝对值越大的地方，重力势能占机械能的比例越小，其变化对机械能守恒所要求的动能（角速度）变化也就越不明显。

    驻点 → 吸引子 (attractor) / 排斥子 (repeller)

    随着维度的升高，驻点的存在，也就是“所有维度的零斜率线相交于某点”这一要求越来越难满足。与此同时，有的时候不需要这么严格的条件，系统也会出现相对稳定的行为。

    所以稳定驻点的概念，被放松成了吸引子，也就是相空间中满足下面三条的子集：

    1. 不变 (invariant)：初值位于吸引子内的系统，其之后时段的轨迹也都位于该吸引子内。
    2. 吸引 (attractive)：初值位于吸引子外的系统，经过时间的演化会被吸引到附近。
    3. 极小 (minimal)：吸引子内部，不存在满足前两条的子集。

    前面讲过的线性系统的驻线，如果是稳定的，就符合吸引子的定义。

    同样类比于驻点，与之相反的相空间结构叫做排斥子。

    极限环 (limit cycle)

    稳定极限环是吸引子中的一种，不稳定极限环是排斥子中的一种。

    我们当初上课时候的例子是一个极坐标中的动力学系统：

    {r˙=dr/dt=r+r3−r5θ˙=ω+br2\begin{cases} \dot r = \mathrm dr/\mathrm dt = r+r^3-r^5\\ \dot \theta = \omega+br^2 \end{cases}

    角速度在离原点越远的地方越大，没什么意思；

    半径方面有两个稳定驻点，一个不稳定驻点：

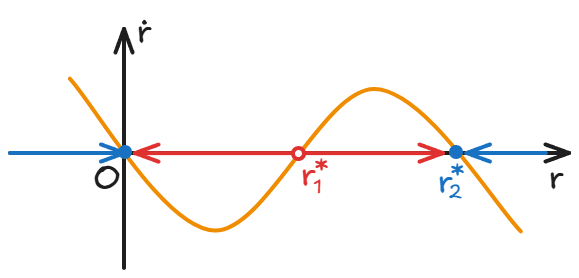
    半径方向上的驻点
    半径方向上的驻点

    而当我们用笛卡尔坐标来表示这个系统的时候：

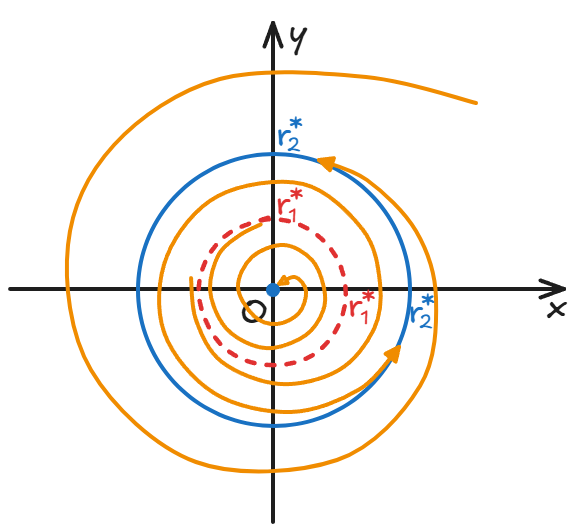
    笛卡尔坐标系中的极限环
    笛卡尔坐标系中的极限环

    以 r2∗r_2^* 为半径的圆就满足我们上面吸引子的定义。初值半径大于 r1∗r_1^* 的轨迹经过足够长的时间，会趋向于绕着蓝色的圆做圆周运动。

    以 r1∗r_1^* 为半径的圆就满足我们上面排斥子的定义。初值半径小于 r2∗r_2^* 的轨迹经过足够长的时间，会趋向于螺旋远离红色的圆。

    这两个圆都是极限环 (limit cycle)。

    下集预告

    混沌 (chaos)

    本文收录于以下合集：