动力学[4] | Chaos 混沌 vs. 真理 vs. 自由

A tentative English translation, not rigorously proof-read yet.

混沌

我们课上对混沌系统的定义是：

Aperiodic behavior in deterministic systems that displays sensitive dependence on initial conditions.

决定论系统中对初值条件高度敏感的非周期行为。

我上学时是个不喜欢看课本的混子，所以我不知道这个定义是我们老师拍脑袋写黑板上的，还是从课本里偷来的。如果是后者，我们的课本是 Steven H. Strogatz 写的《Nonlinear Dynamics and Chaos》

奇异吸引子

“非周期”意味着，动力学轨迹不做周期循环，也不收敛到极限环、驻点，也就存在着其他类型的吸引子，这种吸引子叫做奇异吸引子 (strange attractor)。

说一个连续动力学系统是混沌系统，等价于说系统中存在奇异吸引子。

例子：蝴蝶效应

本文太长，背景介绍先省省，总之一个气象领域的动力学系统（所以在科普中会有“亚马逊雨林中的一只蝴蝶偶尔扇动几下翅膀，就可以在两周以后引起德克萨斯的一场龙卷风”的说法），一番变量替换后：

$$\begin{cases} \dot x=\mathrm dx/\mathrm dt=\sigma(y-x)\\ \dot y=\mathrm dy/\mathrm dt=rx-y-xz\\ \dot z=\mathrm dz/\mathrm dt=xy-bz \end{cases}$$

系统会随着 r 的取值不同而有性质上的变化。

系统的雅各比矩阵：

$$\ \mathbb J=\left( \begin{matrix} -\sigma & \sigma & 0 \\ r-z & -1 & -x \\ y & x & -b \end{matrix} \right)$$

• 0 < r < 1 时，系统的驻点是原点，而且稳定；
• r > 1 时，原点变为不稳定驻点，此时会出现两个新的稳定驻点： $(\sqrt{b(r-1)},\sqrt{b(r-1)},r-1)$ 和 $(-\sqrt{b(r-1)},-\sqrt{b(r-1)},r-1)$
• $r>r_H=\frac{\sigma(\sigma+b+3)}{\sigma-b-1}$ 时开始出现混沌。
  • 最常讨论的参数取值是 $\sigma=10$, $b=8/3$, 此时 $r_H$ 约为 24.76

两个原本稳定的驻点，此时变成奇异吸引子，在两个维度里构成不稳定极限环，在第三个维度稳定。

对这个系统，像前一篇那样手搓动力学轨迹实在是强人所难了，所以直接把维基百科上的数值模拟结果给偷来：

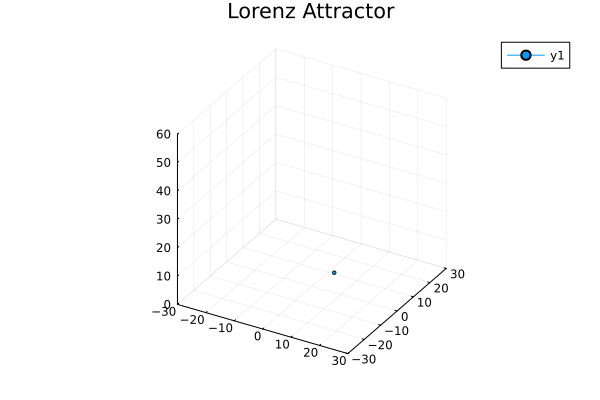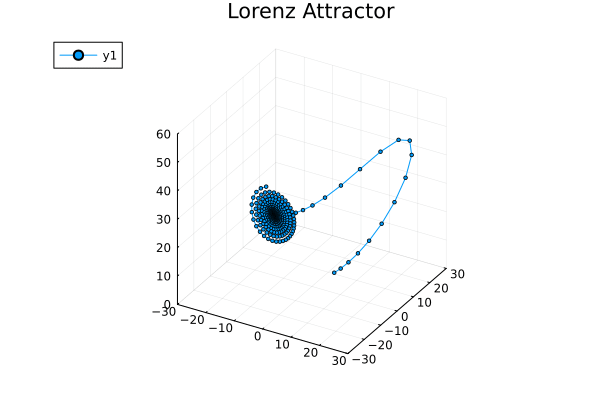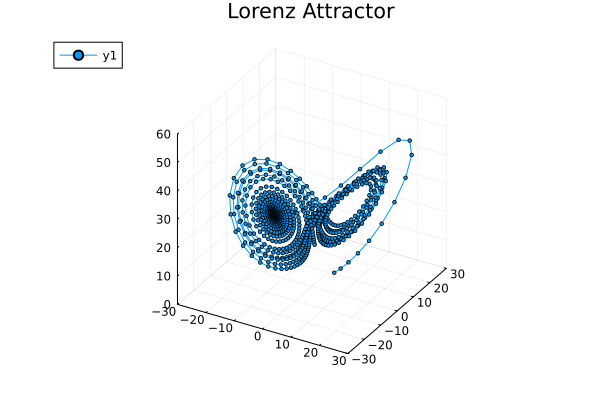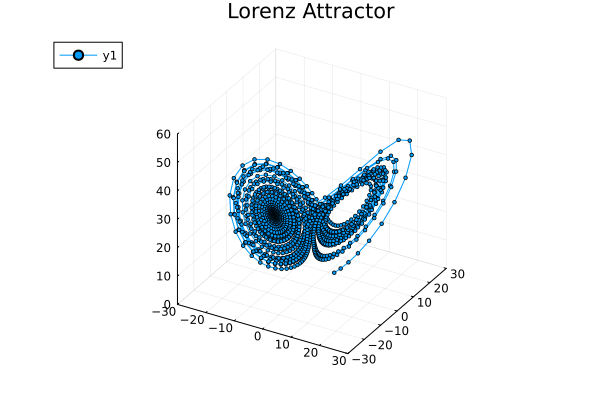
因为任意两条动力学轨迹不能交叉（否则处于交点的系统在下一时刻的去向不明），所以在二维动力学系统里的轨迹不可能绕着一个极限环转了好几圈之后突然去拐去另一个极限环转几圈再拐回来。

连续系统的混沌现象至少需要 3 个动力学维度。

是否“解对初值条件高度敏感”：李雅普诺夫指数 (Lyapunov exponent)

所谓“解对初值条件高度敏感”，往往用李雅普诺夫指数衡量：如果两条动力学轨迹开始时相距 $\delta Z_0$，而在之后的时间里 $|\delta Z(t)| \approx e^{\lambda t}|\delta Z_0|$，就把 $\lambda$ 称为李雅普诺夫指数。

一般来说，吸引子支配的区域，该指数小于 0；排斥子支配的区域，该指数大于 0。

奇异吸引子的“奇异”，就在于它虽然是吸引子，但是李雅普诺夫指数大于 0。

这样，同一系统的两个“差之毫厘”的初值条件，经过一段时间后会“谬以千里”，所以“解对初值条件高度敏感”。

import numpy as np
import matplotlib.pyplot as plt

dt    = 1E-4
N     = int(2.5E5)
delta = 1E-2

sigma = 10
b     = 8/3
r     = 26

f = lambda x,y,z: np.array([
                        sigma * (y - x),
                        r*x - y - x*z,
                        x*y - b*z
                  ])

XYZ0 = np.empty((3,N+1))
XYZ1 = np.empty((3,N+1))
XYZ0[:,0] = np.array([-10.0     ,-10.,20.])
XYZ1[:,0] = np.array([-10.+delta,-10.,20.])
for t in range(N):
    XYZ0[:,t+1] = XYZ0[:,t] + f(*XYZ0[:,t])*dt
    XYZ1[:,t+1] = XYZ1[:,t] + f(*XYZ1[:,t])*dt

plt.figure()
plt.xlabel(   "$t$",fontsize=16)
plt.ylabel("$x(t)$",fontsize=16)
plt.plot(np.arange(N+1)*dt, XYZ0[0], label="$x_0=10.0$")
plt.plot(np.arange(N+1)*dt, XYZ1[0], label="$x_0=9.99$")
plt.legend()
plt.show()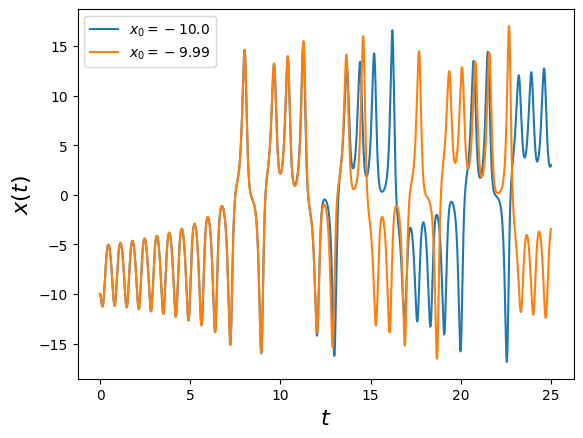

为何“解对初值条件高度敏感”：吸引子的维度

但是另一方面，吸引子把动力学轨迹吸引到相空间的一个子集附近，那么相邻轨迹之间的距离本应该是随时间不断缩小的。一个动力学系统 $\dot{\vec z}=\vec f(\vec z)$ 中，令一堆初值条件在相空间中占据的“体积”为 $V_0$，这一体积随时间的变化率是这么算的：

$$\frac{1}{V}\frac{\mathrm dV}{\mathrm dt}=\vec\nabla\cdot\vec f$$

把洛伦兹系统代入上式，$V(t)=V_0e^{-(\sigma+1+b)t}$ 确实是随时间减小的，甚至可以小到 0。

普通的吸引子里，稳定驻点有 0 个维度，稳定极限环有 1 个维度，它们比所位于的动力学系统，低了至少一整个维度。

经过数值模拟，洛伦兹吸引子的维度大约是 2.05，非整数。

分数维度往往和分形结构有关。洛伦兹吸引子在体积为 0 的情况下依然占据一定空间，（这在离散动力学系统中表现得更明显），吸引子附近的相邻轨迹可能演化到分形的不同枝杈，给了李雅普诺夫指数大于 0 的机会。

真理

“解对初值条件高度敏感”又如何？

绝大多数的科普文章，对混沌系统的描述停留在复读“解对初值条件的高度敏感”，后面没了。就跟学渣写文献综述一样，不敢自行理解，怕被扣一顶稻草人谬误的帽子。

混沌的意义，需要结合《误差的传递，科学之所以科学》中提到的“可证伪性”划界标准来理解：

既然两个初值条件之间的 $\delta Z_0$ 可以任意小，那么我们总能找到两条轨迹，他们初值之间的不同小于测量仪器的误差。此时“它们的初值不同”的断言将无法证伪，我们只能认为它们相等。

但是随着时间的推移，其动力学轨迹的差异会增加到显著大于测量误差的程度。

此时就变成了“一个实验输入，理论会给出多个完全不同的远期行为的断言，无法确定哪个正确”。考虑实验误差才能得到混沌定义中的“不可预测”。

这种不可预测并不是因为理论的失效。如果理论不能用来描述当前的系统，你反而不能断言这里存在奇异吸引子，也就不能断言存在混沌现象了。

这种不可预测也不是因为数值模拟的浮点误差。如果浮点误差导致数值解不能约等于真实解，那这个数值模拟是不该被采用的。一个关于混沌的科普作品如果掉进了计算机浮点数，和“伪随机数/真随机数”的兔子洞，那这个作品大概率是失败了。

牛顿力学 ≠ 机械唯物主义

混沌现象产生于复杂系统，但这个“复杂”并不需要特别复杂。上篇文章中手搓相图的硬棍小球组成的单摆，只要在硬棍小球下面再挂一个自由摆动的硬棍小球，就能成为一个混沌系统，而这只是一个完全由牛顿力学支配的系统。

牛顿力学体系建立之后，拉普拉斯设想了一种妖精 (Démon de Laplace)，妖精知道当前时刻宇宙中每个原子确切的位置和动量，拉氏认为妖精如此便可以知道从过去到未来任意时刻的世界。《青春猪头少年不会梦到理性小魔女》里面双叶理央所遭遇的超自然现象，就是轻小说作者对拉普拉斯妖的一种化用。

现在我们可以反驳说，拉普拉斯的妖精所拿到的，此刻全宇宙所有物质的位置和速度信息，不可能是有无限精度的（毕竟无限并不是一个数字），那么混沌依然会导致宇宙的远期未来无法预测。

此即“可知论不等于命定论”。

诉诸量子力学？

超度拉普拉斯妖的时候，通常的思路是说牛顿力学不适用于微观系统，要想描述原子尺度上的运动需要用量子力学，而量子力学本身就是概率论的，不是决定论的。

然而量子力学的哥本哈根诠释中包括了“对应原理”：大尺度宏观系统的量子物理行为应该近似于经典行为。

当微观粒子的数量达到阿伏伽德罗常数量级之后，粒子之间的物理过程的数量级只会更高。这些过程互相构成对邻近系统的“观察”，互相让对方退相干 (decoherence)。量子力学的预言和经典力学预言之间的差异，最终还是会收敛到宏观测量仪器的误差范围以内。

那些只有量子力学才能解释的新奇物理现象，经典力学往往并未对其断言，所以量子力学对经典力学是一种补充和范式更新，而不是证伪。

而经典力学毕竟是一门科学，而不是纯数学，其正确性是由实验保证的。既然实验证而不伪，那身为决定论而又不可预测的解释还是需要在经典力学内部给出。

哥德尔不完备定理

哥德尔不完备性定理说了，一个包含了皮亚诺公理（自然数的数学基础）的逻辑体系，不可能既自洽又完备。也就是说几乎一切的定量理论，要么内部有矛盾（一个命题和它的否定同时被理论判定为正确），要么存在着没有被纳入理论的正确命题。

数学和自然科学选择了坚决排除内部的矛盾，于是不可避免地要承认自身的有限。在明知“其知也无涯”，永远无法穷举所有真命题的情况下，仍然把有涯之此生投入其中，“即使在人类知识宝库里投进一粒沙子也是伟大的”（居里夫人）。

但另一方面，自然科学的命题又需要有普世性。科学命题应该是全称命题，任何让步性的特设修正需要增加命题的可证伪性，否则就是伪科学。

混沌系统就成了调和两者的一个出口。物理规律等价于所有满足这一规律的解的集合，而一个特定的物理过程只是集合中的一个元素。前者的正确和已知，并不必然能让人选择出任意一个后者。

类似的结果，也见诸赵凯华先生《定性与半定量物理学》中关于“原因不能唯一确定结果时的对称性原理”的讨论。

自由

我们经常看见“知识就是自由”、“知识让人自由”之类的表达，但仔细推敲一下，这些命题的用词相近，表达的意思却大相径庭。

知识本身并不是自由。

恰恰相反，知识会消除自由。一个本来自由的选择，现在知识告诉你，供你选择的选项之间存在对错、优劣。只要知识正确，没有被证伪，不选知识给出的最优解是要吃亏/少赚的，这就是经济学所讲的机会成本。

事前知道吃亏却依然要去做，做完坦然承受后果，这是公民抗命的范畴，是知识之外的价值观给你的自由。当然也可以说价值观/美德是一种知识（苏格拉底），但这种道德知识毕竟不同于硬桥硬马的客观科学。

另一方面，知识确实会让人自由。

对知识的理解包括了对其适用边界的理解，在边界以外的地方，各个选项的对错、优劣无法用知识确定，那里的选择仍然在科学的意义上自由。

更多的知识会揭示出更多像混沌系统一样“已知的未知”，扩展自由的范围。究竟何处自由，我们究竟不知道什么，也是需要谁主张谁举证的。

“除了我们知道的，我们一无所知”的反选法，即便正确也缺少信息量。庄子与惠子游于濠上固然在一时一事上机智，千载之下，终究是躬身格物者，积跬步而致千里。

下集预告

在相图 (phase portrait) 及动力学轨迹这一路之外，动力学的定性和半定量分析还有至少半壁江山，那就是相图 (phase diagram) 及动力学系统的分岔 (bifurcation)。

在连续系统之外，动力学系统至少还有半壁江山，那就是递推映射表示的离散系统，那里一个维度就可能出现混沌。

但是我想夹带的私货都已经夹带完了，所以本系列下一篇何时更新，本号下次更新写什么就都随缘了。本公众号一不开赞赏二不接广告，图的就是个想写什么写什么～

---

本系列开始写作之前，我们系里曾有一个面向公众的周末讲座讲了混沌， （我觉得讲得不算成功……） 以下是我听讲时做的笔记：

Chaos from order, order from chaos

Laplace’s demon, by “French Newton”

Chaos: Poincare 1880 → Mitch Feigenbaum 1970

Turbulence: airplane wing-tip vortex; laminar and turbulent flow

• https://zh.wikipedia.org/zh-cn/%E5%BA%93%E5%A1%94-%E5%84%92%E5%8F%AF%E5%A4%AB%E6%96%AF%E5%9F%BA%E5%AE%9A%E7%90%86

climate depends of total energy balance, and long-term weather patterns

《A random walk down Wall Street》

Feigenbaum: period doubling path to chaos, from programmable HP calculator

population model:

• linear iteration gives exponential growth.
• logistic equation

Feigenbaum’s first constant, universal, but not sure if it is rational

Antikythera mechanism → Sussman and Wisdom, Science 1992

chaos theory vs. Heisenberg uncertainty

chaos ≠ randomness: this talk still does not manage to separate them.