今年刚完结的 4 月番《末日后酒店》(Apocalypse Hotel) 讲的是未来人类因为某种病毒而无法在地球生存,集体乘飞船离开之后,一家酒店的服务机器人们被原主委托继续经营的故事。
非常好看,有一种《相合之物》+《别对映像研出手》的感觉。
第 7 集中,大家决定向太空中发射广告卫星、动能自卫武器,于是狸猫星人的火箭科学家开始在黑板上演算:
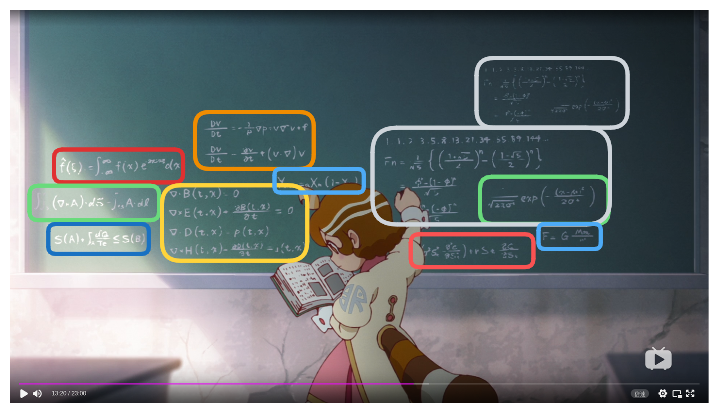 《末日后酒店》第七话
《末日后酒店》第七话
傅里叶变换
左边第一行(红框里)是傅里叶变换
f^(ξ)=∫−∞∞f(x)e2πixξdx
傅里叶变换有多个稍微不同的版本,积分号外面的常数项和指数函数的宗量比较灵活,但是需要保证变换和逆变换的常数项相乘等于 1/(2π),指数相加等于 0.
这一变换把一个以 x 为自变量的函数变换成了另一个以 ξ 为自变量的函数,两个自变量的量纲互为倒数。有些在原空间不方便解的问题,在倒空间里方便很多。一个典型的例子是扩散方程。
斯托克斯公式
左边第二行(绿框里)是斯托克斯公式:
∬S(∇×A)⋅ds=∮∂SA⋅dl
一个向量场 A 的旋度在一个曲面 S 上的积分,等于这个向量场在曲面边缘 ∂S 的闭合线积分。
原图积分号看不清楚,而且向量场 A 没标箭头。
热力学第二定律
左下角(蓝框里)的不等式是热力学第二定律:
S(A)+∫ABTδQ≤S(B)
公式中的积分里的微分号写作 δ,因为吸热放热是一个过程量而非状态量,积分的结果取决于从 A 到 B 的具体方式,这也是中间是不等号的原因。只有可逆过程才能让等号成立。
不可压缩流体的纳维·斯托克斯方程、随体导数
左起第 2 列上方(橙色框里)的两行,第一行应该是不可压缩牛顿流体的纳维·斯托克斯方程,基本是从牛顿第二定律经过变量替换直接得到的:
ρDtDv=DtDv=−∇p+μ∇2v+f∂t∂v+(v⋅∇)v
动画中的写法不同于此处,这里的写法是从维基百科上偷来的。
第二行是随体导数 DtD 的定义。流体力学里有两种视角,
- 一种是取一段宏观无穷小的流体,跟随着它的移动,考察其受到的外力而得知其运动状态,这种视角叫做拉格朗日视角;
- 另一种是置身流体外,描述惯性系下(x, y, z) 位置的地方的流体在 t 时刻的速度,这种视角叫做欧拉视角。
前者建模的时候更符合直觉,后者表达出来更直观。沟通两者的桥梁就是随体导数。
物理专业不学流体力学,这是我本科时跑去数学系 看美女 蹭课时听到的。随体导数的推导方法已经不记得了,以后有时间去翻翻笔记。
麦克斯韦方程
狸猫星人头左边(黄框内)的四条公式就是麦克斯韦方程组:
∇ ⋅ B(t,x)=0∇×E(t,x)+∂t∂B(t,x)=0∇ ⋅ D(t,x)=ρ(t,x)∇×H(t,x)−∂t∂D(t,x)=j(t,x)
用来描述电场和磁场的动力学。动画中仍然没有向量符号,B, E, D, H 场没有向量符号也就罢了,毕竟大家基本都默认它们是向量;但是 x 没有箭头就不应该了,一维空间里谈不上散度,也定义不了旋度。
逻辑斯蒂 (logistic) 动力学
狸猫星人头顶(蓝框内)是逻辑斯蒂 (logistic) 动力学方程,这是一种用递推公式表示的离散动力学系统:
Xn+1=aXn(1−Xn)
其中常数 1 可以变成一个可变参数 κ,当初值位于 0 和 κ 之间时,这个动力学系统可以模拟出动物群体数量的 S 形增长曲线,κ 就是生态系统对这一物种的环境承载力。
把 κ 固定成 1,可以方便讨论参数 a,在某些取值范围内,这个动力学系统可以表现出混沌现象。
你问我这个公式为什么出现在这里,我不知道啊……
图片重用
右侧两个灰框里的内容相同,只是做了一下缩放。这种做法严重违反学术道德,在学术出版物中是要撤稿的。
在学术出版物中重用他人的图片,哪怕是自己早先文章里的图片,也要用符合规范的方式注明引用。
斐波那契数列
灰框里面,浅绿色框以外的部分是斐波那契数列:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
前两项是 1, 1,此后每一项是其他两项之和: Fn=Fn−1+Fn−2, n>2
以上是递推公式。它的通项公式就是黑板上的:
Fn===51{(21+5)n−(21−5)n}5ϕn−(1−ϕ)n5ϕn−(−ϕ)−n
其中 ϕ 是黄金比例 21+5
你问我这个公式为什么出现在这里,我不知道啊……
正态分布
灰框里面的绿框里是正态分布的概率密度:
2πσ21exp(−2σ2(x−μ)2)
μ 是该分布的期望,σ 是该分布的标准差。
指数前面的系数,是为了保证整个表达式的在整个实数轴上的积分为 1. 而要求出指数项的积分,需要先将系统升到 2 维,然后将笛卡尔坐标系换成极坐标系。
∫−∞+∞exp(−2σ2(x−μ)2)dx=======(∫−∞+∞exp(−2σ2(x−μ)2)dx)2∫−∞+∞exp(−2σ2(x−μ)2)dx∫−∞+∞exp(−2σ2(y−μ)2)dy∬−∞+∞exp(−2σ2(x−μ)2+(y−μ)2)d(x−μ) d(y−μ)∫02π∫0+∞exp(−2σ2r2) rdr dθ2π⋅21∫0+∞exp(−2σ2r2)d(r2)π(−2σ2)[−exp(−r2/2σ2)]∣0+∞2πσ2
万有引力
四大基本相互作用之一:
F=Gr2Mm
整个黑板最能和火箭扯得上关系的公式了。
(可能是)Black–Scholes–Merton 方程
狸猫星人右肩旁边(红框内)的公式被挡住了一部分,只剩下:
… (σ2St2∂St2∂2ζ)+rSt∂St∂ζ
问了一下 ChatGPT,得知可能是 Black–Scholes–Merton 方程:
∂t∂V+21σ2S2∂S2∂2V+rS∂S∂V−rV=0
但是这个方程是用来估算金融市场里欧式期权的价格的——
你问我这个公式为什么出现在这里,我不知道啊……
